Calculate the flux of the indicated electric field vector through the circle

[cwatki14]

Calculate the flux of the indicated electric field vector through the surface. (E = 130, = 66.0°.)

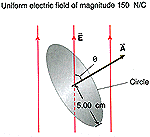I know the differential equation for flux d\phi= A \bullet d S
[/B]

My textbook told me that "if there is zero total charge within the closed surface S, there is no net flux of the electric field vector through S."
I guessed that the total flux was 0, but that was wrong...
Or maybe it's
\int (from O to .05m) <130,0> \bullet \pi r ^2(<cos60,sin60>)
But I'm not really even sure how to do an integral with a dot product(would you dot them first?), and I'm fairly certain that's wrong...

Any ideas?

 

[tiny-tim]

Welcome to PF!

Hi cwatki14! Welcome to PF!

(type \cdot, not \bullet )

My textbook told me that "if there is zero total charge within the closed surface S, there is no net flux of the electric field vector through S."
I guessed that the total flux was 0, but that was wrong...

A "closed surface" mans a surface with no boundary (like a sphere), but S does have a boundary … it's the circle round S

(I suspect you're confusing this with a topologically closed (as opposed to open) surface … a surface which includes its boundary)

 

[cwatki14]

So is the flux then
\int(130)(sin\pi/3)(\pi)(dr)^2
and then you take the integral to get
130*sin\pi/3*\pi\intdr^2
and I'm not sure when to go from here...

 

[cwatki14]

So I was pretty sure I had it when I realized you can just take the dot product between the area and the electric field.

Therefore I was led to this answer.
A dot E= 130 * pi(.05)^2 * cos 66
Which is equal to the magnitude of the electric field multiplied by the magnitude of the area multiplied by the angle in between the two vectors (reference the pic above). However, my online homework program quickly told me I was wrong! Blergh! Any suggestions?

 

[tiny-tim]

Hi cwatki14!

(have a pi: π and a dot: · and try using the X² tag just above the Reply box )

So I was pretty sure I had it when I realized you can just take the dot product between the area and the electric field.

That's right … you only need to integrate if the field isn't constant, or if the surface (or its boundary) isn't planar.

Therefore I was led to this answer.
A dot E= 130 * pi(.05)^2 * cos 66
Which is equal to the magnitude of the electric field multiplied by the magnitude of the area multiplied by the angle in between the two vectors (reference the pic above). However, my online homework program quickly told me I was wrong! Blergh! Any suggestions?

Looks ok to me

(Are you sure it isn't 150, not 130?)