Calculating acceleration from electric motor

[vinrow]

I am in the process of designing an electric motorcycle, and would like to approximate the acceleration from various motors to inform my decision. I have written simple software to produce performance graphs, but my results seem a bit off - so i'd like to check my calculations.

Here is the basic setup:

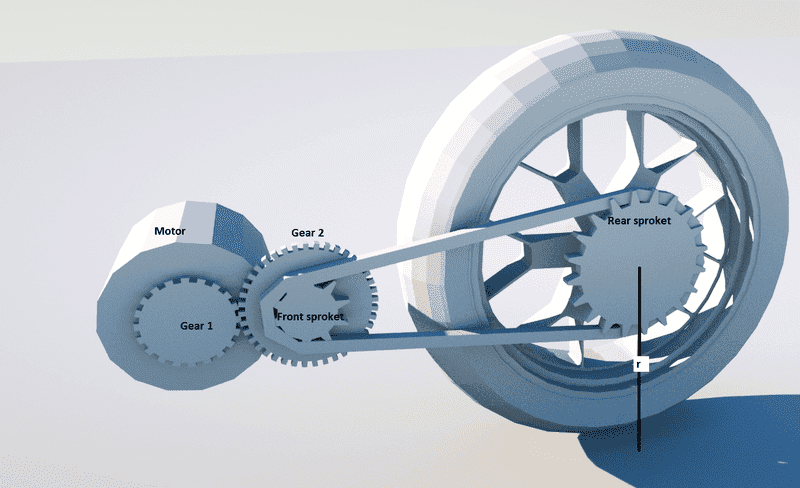
To simplify things I first calculated the effective radius of the wheel based on the gearing (as if driving the wheel directly from the motor):
r = Wheel radius / (Gear2/Gear1) * (RearSproket/FrontSproket)

Then used: Motor torque (T) = Fd and F=ma to get a = T/mr.

From this I calculate velocity at time intervals using: v = u+at and distance: S=ut + 0.5at^2

Now the bit where I think I'm going wrong (if not already) - Incorporating drag.
Using the drag equation: https://wikimedia.org/api/rest_v1/media/math/render/svg/144ce01ab76e5e8a0662dbf0f5b922abfa726e9c I am using a coefficient of 0.5, and area of 0.4m^2.
When calculating the torque at the rear wheel, I'm doing (Motor torque * 0.9) - (Drag force * r). The 0.9 is just to add a bit of mechanical loss. But I can't work out if I'm applying the drag correcly. Any input welcome.

 

[billy_joule]

Drag force does not cause a torque about the motor shaft as your equation implies. The drag force had nothing to do with the gear ratio.

To find the net force on the bike the drag force should be subtracted from the force the wheel applies to the road.

You will also need to account for the torque curve of the motor, electric motors generally produce max torque at zero rpm and zero torque at max rpm.

 

[jack action]

Drag force does not cause a torque about the motor shaft as your equation implies. The drag force had nothing to do with the gear ratio.

Instead of doing $ma = \frac{T}{r} - F_d$, he seems to do $mar = T - F_d r$, which gives the same results.

@vinrow, you should check this acceleration simulator and the theory behind with it.

 

[billy_joule]

Instead of doing $ma = \frac{T}{r} - F_d$, he seems to do $mar = T - F_d r$, which gives the same results.

Ah yes, I see.

 

[CWatters]

One option might be to tow an un powered bike behind a car. Measure the tension in the tow rope and you can measure the power required at various speeds or during acceleration etc. Use a long rope or other methods to avoid slipstream effects.

Won't account for all losses (eg those in the motor) but even so should give good data.

 

[vinrow]

Thanks for the input everyone, so the calculations seem correct. @billy_joule yes I am using torque curve data obtained from the manufacturer of the motor. The main reason for the simulation is because they have two similar motors and I'm not sure which would be best.
@jack action Thanks for the link. After looking at it I think my inaccuracies are due to not having enough frictional losses, and also not taking into consideration things like rotational inertia.
@CWatters Interesting idea but probably overkill for what I need. My drag coefficient and area are taken from wind tunnel data of the bike I would use - so should be at least in the ball park. I don't need amazing precision, just enough to evaluate the motors I'm looking at.