Calculating Angle of Wheel Rotation for Rolling Bicycle

[nan0]

Homework Statement

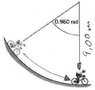
A bicycle is rolling down a circular hill that has a radius of 9.00m. The angular displacement of the bike is 0.960rad. The radius of each wheel is 0.400m. What is the angle (in radians) through which each tyre rotates ?


Notes on question :
- wheels are in rolling motion (involves rotation)
- bicycle speed and wheel speed is angular

Homework Equations

angle = 1/2 (Wo + W)t
angle = WoT + 1/2(angular displacement)Tsquared

The Attempt at a Solution

From theoretical point, would jus like to know how to approach the question as the only given data is displacement and length. If I could calcualte 2 more variables I can use a kinematics equation.

 

[Redbelly98]

Welcome to PF

I don't understand the situation being described. In particular, what does this mean:

The angular displacement of the bike is 0.960rad.​

Does this refer to the bike's position on the circular hill? If so, does a displacement of 0rad correspond to the top or bottom of the hill, or somewhere else? Is the hill itself a full circle, a semicircle, or some other portion of a circle?

I suspect the key is to figure out over what distance the bike travels. Angular velocities and accelerations don't seem to play a role here.

 

[nan0]

Thanx for the welcome

The angular displacement refers to the distance the bicycle has traveled on the circular path.

The hill could be imagined be a circle. I tried to approach the question from a rolling motion point of view, whereas the linear speed and angular speed has a relation, but seeing that the bike is not traveling on a straight line it's not the rite way.

Doesnt the bike's angular displacement relate to the wheel's angle ? Seeing that both object are rotating around a fixed axis

 

[Redbelly98]

I can't see your figure yet, but it sounds like you'll need the arc-length formula. That's the formula which relates arc-length, radius, and angular displacement for a circle.