sudnak
- 3
- 0
Hello All,
I am in the process of creating a 33' tall chaotic pendulum, and cannot find any calculations for the buckling strength of pipe. The pendulum swings from side to side, but is stopped as it goes too far one way or another by a limiting cable attached to a sleeve over the pendulum. So, essentially I have a pipe supported on one end and free on the other, and there will be a force applied to the end of the pipe. I need to know how to calculate the amount of force that different size pipes can take before they buckle. The force from the load, calculated at the fixed end of the pipe, is about 2800N. See picture for details. So, what formulas can I use to find this? Would I calculate section modulus and moment of inertia? Thanks for all the help!
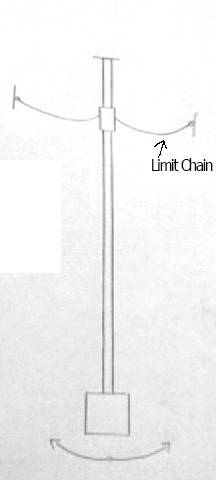
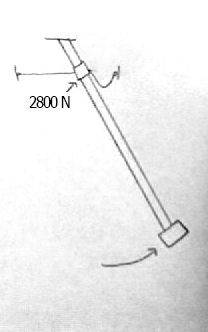
I am in the process of creating a 33' tall chaotic pendulum, and cannot find any calculations for the buckling strength of pipe. The pendulum swings from side to side, but is stopped as it goes too far one way or another by a limiting cable attached to a sleeve over the pendulum. So, essentially I have a pipe supported on one end and free on the other, and there will be a force applied to the end of the pipe. I need to know how to calculate the amount of force that different size pipes can take before they buckle. The force from the load, calculated at the fixed end of the pipe, is about 2800N. See picture for details. So, what formulas can I use to find this? Would I calculate section modulus and moment of inertia? Thanks for all the help!