Calculating Distance of Ball Launch in Semicircular Chute

[EaGlE]

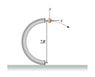
A ball is launched up a semicircular chute in such a way that at the top of the chute, just before it goes into free fall, the ball has a centripetal acceleration of magnitude 2g.

1.)How far from the bottom of the chute does the ball land? Your answer for the distance the ball travels from the end of the chute should contain R.

D=__________


can someone help me start this? i really don't know where to start this problem from.

 

[Sirus]

Use what you know to find the velocity of the ball at the top of the chute, then treat it as a projectiles question, where you know the initial velocity, the initial height (2R), and the acceleration due to gravity: how much time does it take for the ball to reach the ground when considering only its accelerated vertical motion, and how far will it have traveled horizontally during this time?

 

[Pyrrhus]

Remember:

A_{c} = \frac{V^2}{R}

where A_{c} is Centripetal Acceleration.

 

[EaGlE]

i don't remeber us doing this in class at all, so i read the chapter relating to this subject many times, and it's confusing for me.

ok i know that a = 9.8m/s^2, initial velocity = 0, initial height = 2r

so...

x(t) = 2r + 0 + 1/2(-9.8)t^2
2r = -4.9t^2

sorry but i have no clue on what to do...

A_{c} = \frac{V^2}{R}


we don't know velocity right? ...

 

[Pyrrhus]

Well the Problem gives you the A_{c} and in the graphic you can see the radius is R, how can you use the equation i gave you, in order to find the speed at the top? and then use that speed for the projectile motion part.