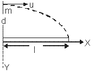Calculating Force on an Electron Projected Towards a Charged Conducting Plate

[Tanya Sharma]

Homework Statement

An electron is projected from a distance d and with initial velocity u parallel to a uniformly charged flat conducting plate as shown. It strikes the plate after traveling a distance l along the direction of projection. The surface charge density of the conducting plate is equal to

Ans :dε₀mu²/el

Homework Equations

The Attempt at a Solution

Electric field of the conducting plate = σ/ε₀

Force on the electron in y direction = eσ/ε₀

a_y = eσ/mε₀

l=ut and d=(1/2)a_yt²

Solving these ,I get σ = 2dε₀mu²/el² ,but this is incorrect.

I would be grateful if somebody could help me with the problem.

 

[ehild]

Hi Tania,
It looks correct for me, but do not forget the parentheses.

ehild

 

[Tanya Sharma]

Hello ehild

Thank you very much :)

 

[haruspex]

Note that the given answer must be wrong since it has the wrong dimensionality.

 

[Tanya Sharma]

Okay . Thanks for the input .