Calculating Op-Amp Input Resistance in Non-Ideal Circuits | Tips & Tricks

[gambit1414]

Certain questions involve finding input resistance for circuits (e.g. inverting or non-inverting configuration). I know ideally the op-amp has infinite input resistance but i don't know how i would be able to calculate the input resistance for non-ideal circuits? Thank You.

 

[The Electrician]

Give an example of a circuit where you are asked to determine the input resistance, and we can help.

Post an image of a circuit schematic.

 

[gambit1414]

Ok, unitiled1 the question asks to find expression for input resistance taking into account the finite open-loop gain A. And regarding untitled2, like i know that's the inside of an op-amp and that ideally the resistance is supposed to be infinite, and idealy V+ = V-, so how are you going to get a gain if the v-inputs are the same? isn't, Voutput = A(V+ - V-)? And it would help if someone could elaborate on untitled2 diagram because i don't see the point of having the Rout resistor because wouldn't that lower your gain? Or is that there so we can measure the the Vout? Thanks a lot.

 

[The Electrician]

I can't see your images until they have been approved.

To allow me to see them sooner, upload them to an image hosting site, such as:

http://www.freeimagehosting.net/

and post the link to the images in the forum.

 

[Redbelly98]

For the 1st circuit, point 1 is considered a "virtual ground". This is because the op-amp's feedback keeps the - and + terminals at nearly the same potential, and the + terminal is grounded.

That fact greatly simplifies things, and helps with figuring out the input impedance.

 

[The Electrician]

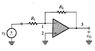
For the first one, proceed as follows to solve the circuit.

Using KCL, calculate the current in the two resistors and set their sum, which occurs at V1, equal to zero.

(V1-Vi)/R1 + (V1-Vo)/R2 = 0

Also knowing that Vo = -A*V1 (A is the opamp gain) we can substitute this in the first equation.

(V1-Vi)/R1 + (V1 + A*V1)/R2 = 0

After a little algebra, we get:

V1 = Vi * R2/(R2 + A*R1 + R1)

From this we can get the current into R1 from Vi:

Ii = (Vi-V1)/R1 = Vi*(1 - R2/(R2 + A*R1 +R1))/R1

The resistance seen at the left end of R1 is the voltage there, Vi, divided by the current into R1:

Zin = Vi/Ii = R1*(R2+(1+A)*R1)/((1+A)*R1) = (R2+(1+A)*R1)/(1+A)

Notice that in the case of an ideal opamp where A -> infinity, this expression reduces to R1, which is what you would expect the input resistance to be.

To account for the finite open loop gain, substitute an expression for finite open loop gain for the symbol A in the expression above.

For example, if the opamp has a simple one pole roll off, then a suitable expression for the finite gain would be:

A = Ao/(1 + s*to) where Ao is the DC gain and to is the time constant of the roll off.

You can solve your second example similarly.

 

[The Electrician]

And it would help if someone could elaborate on untitled2 diagram because i don't see the point of having the Rout resistor because wouldn't that lower your gain? Or is that there so we can measure the the Vout? Thanks a lot.

I see that what I said in my previous post doesn't really apply to the second image.

The second image is just showing a simple model for an opamp open loop.

The output resistance has a very small effect on circuit behavior when an opamp is used with substantial feedback, as is the usual case. Even though the effect is usually negligible, it can be included in an analysis if you want.