rdn98
- 39
- 0
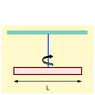
A uniform meter stick is hung at its center from a thin wire. It is twisted and oscillates with a period of 5 s. The meter stick is then sawed off to a length of 0.76 m, rebalanced at its center, and set into oscillation.
******************
With what period does it now oscillate?
Ok, I know that the period for a torsion pendulum T=2pi*sqrt(I/k)
Where I is moment of inertia
and K is the torsion constant
Two things I am stuck on.
To calculate the moment of inertia => 1/12 ML^2
I need to konw the mass of the rod...unless this mass drops out of the calculations, I don't know what to do
Also, the torsion constant. I do not konw what that is either, unless that too also drops out of my calculations. A little guiadance here greatly appreciated.
******************
With what period does it now oscillate?
Ok, I know that the period for a torsion pendulum T=2pi*sqrt(I/k)
Where I is moment of inertia
and K is the torsion constant
Two things I am stuck on.
To calculate the moment of inertia => 1/12 ML^2
I need to konw the mass of the rod...unless this mass drops out of the calculations, I don't know what to do
Also, the torsion constant. I do not konw what that is either, unless that too also drops out of my calculations. A little guiadance here greatly appreciated.