ElectricMile
- 31
- 0
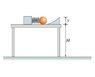
Calculate vr, the speed of the ball when it leaves the launching ramp. Express the speed of the ball in terms of k, s, m, g, y, and/or H.
i know it will contain m, y and k
also
With what speed will the ball hit the floor? Express the speed of the ball in terms of k, s, m, g, y, and/or H.
i am so confused when it comes to creating these "expressions" i don't even know where to begin or what the heck to do.
i know it will contain m, y and k
also
With what speed will the ball hit the floor? Express the speed of the ball in terms of k, s, m, g, y, and/or H.
i am so confused when it comes to creating these "expressions" i don't even know where to begin or what the heck to do.