- #1
KiNGGeexD
- 317
- 1
I had this question given in my class
A spectral line from iron (mass 55.934 amu) atoms in the sun is measured as 637.4 nm. It's width is measured to be 0.053 nm. Calculate the temperature of the sun?Now I done this using a formulae I was given but it yielded an answer no where near 5778K
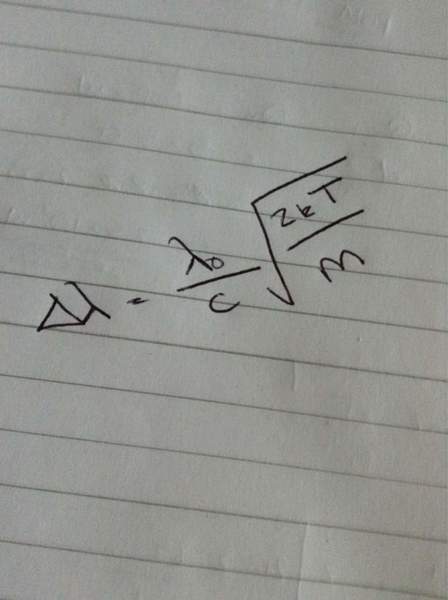 Above is the equation I actually used where delta lambda is width and lambda 0 is wavelength? I'm confused as to why my answer is two orders of magnitude out? Is it supposed to be like this as the iron atoms will be hotter because of the chemical composition or am I supposed to be able to get roughly 6000K with this question? I know there is little iron compared to hydrogen and helium in the sun so could that have something to do with it? So many questions
Above is the equation I actually used where delta lambda is width and lambda 0 is wavelength? I'm confused as to why my answer is two orders of magnitude out? Is it supposed to be like this as the iron atoms will be hotter because of the chemical composition or am I supposed to be able to get roughly 6000K with this question? I know there is little iron compared to hydrogen and helium in the sun so could that have something to do with it? So many questions
Anyways thanks for your help in advanced I hope you can help
A spectral line from iron (mass 55.934 amu) atoms in the sun is measured as 637.4 nm. It's width is measured to be 0.053 nm. Calculate the temperature of the sun?Now I done this using a formulae I was given but it yielded an answer no where near 5778K
Anyways thanks for your help in advanced I hope you can help