motivehunter
- 12
- 1
Hi everyone,
I just completed my bachelor's in mechanical engineering and have taken up a small project which involves a pedal assisted bicycle operating on both torque and cadence values.
Having completed the design and relevant estimations, I have now gotten stuck at a problem which seems to threaten my very understanding of the concept of torque. I am trying to calculate the torque required of the electric motor used by the bicycle and have taken the following design approach:
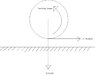
To determine the maximum possible torque required of the motor, it is assumed that the bicycle is moving up a plane inclined at 35 degrees to the horizontal. As the force which is the weight component acting parallel to the inclined plane (W*Sin(alpha) where alpha is the angle of inclination) acts along the centre of gravity and rear axle of the bicycle, it is assumed to have no torque in resisting the motion of the bicycle. However, the frictional forces resisting the motion of the rear wheel (which being the driving wheel, is being studied) apply a resisting torque by attempting to rotate the wheel in the counter-clockwise direction. The maximum torque required is therefore that torque required to be applied on the rear wheel which will just about counter the effect of this 'resisting torque'. Please look at attached images to better understand this.
In my model, I know that 60% of the bicycle's weight acts on the axle of the driving wheel and I have used this to calculate the resisting torque which is given by Tau = mu * 0.6 * W * Cos(35) * r where 'r' is the radius of the wheel. The resisting torque value comes up to be 167.22 Nm.
Is this approach a valid approach to determining the torque? If not, could you please point out the flaws in this approach so that I may correct my understanding of this?
Thank you in advance!
I just completed my bachelor's in mechanical engineering and have taken up a small project which involves a pedal assisted bicycle operating on both torque and cadence values.
Having completed the design and relevant estimations, I have now gotten stuck at a problem which seems to threaten my very understanding of the concept of torque. I am trying to calculate the torque required of the electric motor used by the bicycle and have taken the following design approach:
To determine the maximum possible torque required of the motor, it is assumed that the bicycle is moving up a plane inclined at 35 degrees to the horizontal. As the force which is the weight component acting parallel to the inclined plane (W*Sin(alpha) where alpha is the angle of inclination) acts along the centre of gravity and rear axle of the bicycle, it is assumed to have no torque in resisting the motion of the bicycle. However, the frictional forces resisting the motion of the rear wheel (which being the driving wheel, is being studied) apply a resisting torque by attempting to rotate the wheel in the counter-clockwise direction. The maximum torque required is therefore that torque required to be applied on the rear wheel which will just about counter the effect of this 'resisting torque'. Please look at attached images to better understand this.
In my model, I know that 60% of the bicycle's weight acts on the axle of the driving wheel and I have used this to calculate the resisting torque which is given by Tau = mu * 0.6 * W * Cos(35) * r where 'r' is the radius of the wheel. The resisting torque value comes up to be 167.22 Nm.
Is this approach a valid approach to determining the torque? If not, could you please point out the flaws in this approach so that I may correct my understanding of this?
Thank you in advance!