has1993
- 7
- 0
Homework Statement
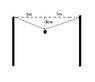
As shown in attachment a steel cable is stretched between two poles. In 20°C temperature the cable remains horizontal (the length of the cable 10m). At a higher temperature θ°C the cable bends like in attachment. The lamp hanging from the mid-point could be thought as weightless. The linear expansion coefficient for steel is 12 * 10^-6. What is the value of θ?
Homework Equations
l' = l [1 + αθ] ------- 1
The Attempt at a Solution
I first used pythagorian to find the expanded length so,
L^2 = 25 + 64 * 10^-4
that gives L = 5.0064
so the total expanded length 2L = 10.0128
And applying it to the (1) equation
I get a value for θ = 126 °C ! obviously absurd.
So anyone got a hint on what I'm doing wrong?