Bolter
- 262
- 31
- Homework Statement
- See below
- Relevant Equations
- pressure = rho x g x h
specific weight = rho x g
Hi everyone!
How do I go about solving this problem?

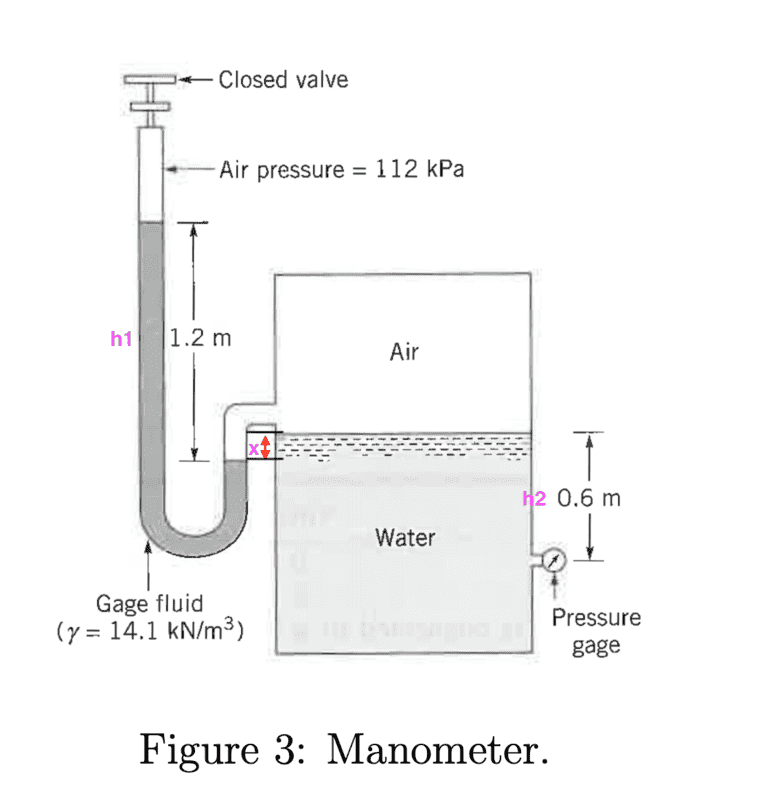
I tried working out the gauge pressure using this but I have a few unknowns which won't make this possible such as what is the length of x which I labelled in the figure

Any help would be appreciated! Thanks
How do I go about solving this problem?
I tried working out the gauge pressure using this but I have a few unknowns which won't make this possible such as what is the length of x which I labelled in the figure
Any help would be appreciated! Thanks