Can Different Curvatures Exist in Equilibrium for Fluid-Filled Pipe?

[member 428835]

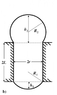
Suppose we have a pipe of some length $2L$ and at the ends there is to spherical caps of fluid, as shown in the attachment. Is it possible for the two ends to have different curvatures in equilibrium?

My initial thoughts are no, since pressure is proportionate to curvature (Young-Laplace) and I don't think a pressure gradient would exist in equilibrium. What do you think?

 

[John Morrell]

You can have a pressure gradient in equilibrium. You just need some other force acting to balance out the force from pressure. For example, water at the bottom of a pool is at much higher pressure than water at the top of a pool. Air pressure is much higher on the surface of the Earth than 2 miles above the surface. If your pipe is held vertically, than you would by necessity have a pressure gradient which would be equal to the density times Earth gravity times the depth.

Furthermore, you could have different atmospheric pressures applied to the different ends, though that might be reading way too much into it.

 

[member 428835]

Hmmm yea that makes a lot of sense. So in the absence of gravity and assuming atmospheric pressure to be constant, for equilibrium to exist the curvatures would have to be constant at both ends?

 

[John Morrell]

Assuming no other forces on the fluid in the pipe, than we'd have to assume zero pressure gradient and thus equal curvatures.

 

[member 428835]

Thanks!

 

[John Morrell]

This just comes down to a definition of equilibrium. We're assuming all forces in the fluid are canceling each other out, so that the net force is zero. Pressure gradients indicate a force, so for a pressure gradient to exist the fluid either has to have some other force at work, or it has to not be in equilibrium.