Jason24
- 5
- 0
Homework Statement
Require various values from cantilever beam analysis including
Bending moment
K stiffness
2nd moment of inertia
Max stress
Homework Equations
Shown below
The Attempt at a Solution
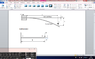
Here is my attempt at this question but I am unsure about units and therefore my answers?Bending moment
Image attached below
Calculated as follows:
L=0.24M
L2=0.02M
P=-0.0049KN
FX=0
FY=0
RAx=0 (No horizontal forces)
+Ray-0.0049=0
M=0
- (0.0049) (0.25) +Ma=0
Ma=1.176x10-3
Second moment on inertia
Ix=bh^3/12 = (30) (260) ^3/12 = 43.94x10^6 (439.4mm^4)Neutral axis (Y)
X axis = 6mm hence Y=3mm
Flexural formula
To find max stress
M/I = Sigma/Y
M=1.176x10-3
I=43.94x10^6
y=3mm
Stress= My/I (flexural formula)
Stress = (1.176x10-3) (0.003) = 8.04x10^-14
(43.94x10^6)
K stiffness
K=3EI = (3)(190x10^9)(43.94x10^6)/0.26^3 = 1.425x10^13
l^3
Young’s modulus formula
E= f
e
Ee=f
Strain= Stress/Young’s modulus
Strain= 6.68/190x10^9= 3.51Stress
Stress = W/Z (l-x)
Stress = 4.9/14.64x10-3 (.26 -.24) = 6.69N
E= stress/strain
E=190x10^9
Strain = Stress/E = 6.69x190x10^9 = 3.52x10^-11
Stress = E x Strain = 190x10^9 x 3.52 x 10^-4 = 6.68
Any help is greatly appreciated!
Homework Statement
Homework Equations
The Attempt at a Solution
Attachments
Last edited: