Change to polars double integral

[Kuma]

Homework Statement

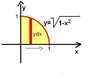
Here is the question

Homework Equations

The Attempt at a Solution

So converting to polars by x = r cos θ, y = r sin θ gives me r^5 in the inner integral

but how do you convert the ranges?

y goes from 0 to sqrt 1 - x^2, so that is just r, I could tell just by looking at it, but in a harder question how do you derive the range in terms of r? x goes from 0 to 1, but how do you convert that in terms of θ (an angle)?

 

[vela]

Have you sketched the region of integration?

 

[ehild]

Draw the domain of integration in the x,y plane (like in the figure) and find the ranges of θ and r from there.

ehild