Checking Whether a Force is Conservative Using Integration

[SHISHKABOB]

Homework Statement

Perform the integration, ∫\vec{F}\bullet d\vec{r}, of the following forces along two independent paths, to verify that (a) is conservative and (b) is nonconservative.

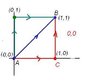
Start from the origin and end at the point (1,1). Take one path as the line x = y; for the other path, take the x-axis to the point (1,0), then the line x = 1 up to the point (1,1).

(a) Verify that \vec{F} = y\hat{x} + x\hat{y} is conservative by integration of two paths, as described above.

(b) do the same to \vec{F} = xy\hat{x} + x\hat{y} to show that it is nonconservative

Homework Equations

The Attempt at a Solution

okay so, I can see that this is a very simple problem, but I have a very simple issue: I don't think I know what it means to "take a path" for an integral.

What should happen is that for the conservative force, I should get the same result for both paths. This shows that the path does not affect the amount of work done.

For the nonconservative force, I should get two different results. This would show that the path choice affects how much work is done.



So my base assumption is that

\int \vec{F}\bullet d\vec{r} = \int F_{x}dx + \int F_{y}dy

so the first path is along x = y to (1,1)

\int F_{x}dx + \int F_{y}dy from 0 to 1 for both.

Then the second path is \int F_{x}dx + \int F_{y}dy from 0 to 1 for x and 0 to 0 for y

plus

\int F_{x}dx + \int F_{y}dy from 0 to 0 for x and 0 to 1 for y

so I get x + y in both cases, so far so good

I then do the same thing for \vec{F} = xy\hat{x} + x\hat{y}

but also get the same result for both paths. This leads me to believe that I don't have any idea what "integrating along a path" means.

 

[szynkasz]

Check a definition of a line integral

 

[ehild]

Calculate the definite integral along the blue line and also along the red one.

Along the blue line, x=y. Therefore dy=(dy/dx)=dx.
In case a), F_x=y, F_y=x, so F_x=x, F_y=x along the line.

\int_{(0,0)}^{(1,1)}{F_xdx+F_ydy}=\int_{0}^{1}{(x+x)dx}


In case b), F_x=xy=x², F_y=x.
\int_{(0,0)}^{(1,1)}{F_xdx+F_ydy}=\int_{0}^{1}{(x^2+x)dx}

ehild


Following the red line, you integral from (0,0) to (1,0) first, then from (1,0) to (1,1)

\int_{(0,0)}^{(1,1)}{(F_xdx+F_ydy}=\int_{(0,0)}^{(1,0)}{F_xdx}+\int_{(1,0)}^{(1,1)}F_ydy

Along the horizontal line y=0. Along the vertical line x=1.

Case a): \int_{(0,0)}^{(1,1)}{F_xdx+F_ydy}=\int_{(0,0)}^{(1,0)}{ydx}+\int_{(1,0)}^{(1,1)}xdy=\int_{0}^{1}{0*dx}+\int_{0}^{1}1*dy

Case b):
\int_{(0,0)}^{(1,1)}{F_xdx+F_ydy}=\int_{(0,0)}^{(1,0)}{xydx}+\int_{(1,0)}^{(1,1)}xdy=\int_{0}^{1}{0*dx}+\int_{0}^{1}1*dy

Try to do the integral also along the green path.


ehild