wilsondd
- 7
- 0
Homework Statement
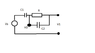
As part of a larger problem, I'm trying to understand the dynamic equations of the attached circuit with two capacitors and one resistor and a voltage source. When I use Kirchoff's Current Law at nodes V0 and V1, I get the following equations.
Homework Equations
See Attachment for circuit diagram
The Attempt at a Solution
When I use Kirchoff's Current Law at nodes V0 and V1, I get the following equations.
0 = (dVs/dt-dV1/dt)*C1 - (V1-V2)/R - (dV1/dt-dV2/dt)*C2
0 = (dV1/dt-dV2/dt)*C2 + (V1-V2)/R
I have a feeling that this approach is wrong though, since I can't solve the equation when C1 = C2. I would be very appreciative if someone could tell me where I'm going wrong.