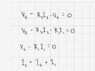Circuit with resistor, switch and capacitor

[johann1301h]

Homework Statement

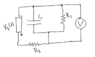
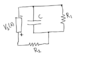
We have a circuit with a battery, two resistors, a switch and a capacitor. We assume that the battery has a switch so that we can choose whether it should be a voltage source for the circuit.

a) At time t = 0, we put on a voltage Vs
over the battery in the circuit. What is the current over the resistors and over the capacitor?

b) At time t = 0, we put on a voltage Vs
in the circuit. What is the charge on the capacitor as a function of time? What is the current over R2
as a function of time?

The Attempt at a Solution

I assume that the circle with the V inside is the switch. I guess I have to use
Kirchhoffs first and second law somehow, can someone give me hints? I not sure if understand the different components of the diagram, where is the switch for instance?

 

[gneill]

Usually a circle with a V inside represents a voltmeter. The switch would be associated with the V_s(t) component (the battery).

What have you learned about the basic RC circuit so far?

 

[johann1301h]

Not much, so there is no resistance in the voltmeter?

 

[gneill]

Not much, so there is no resistance in the voltmeter?

The voltmeter, unless stated otherwise, is considered to be ideal and does not affect the circuit at all. It effectively has infinite resistance (open circuit).

You'd best go to your class notes and textbook and look at the sections that describes capacitors and the RC circuit. There's a formula or two you'll need.

 

[johann1301h]

Yes, sadly the course I'm taking is horrible, and there really isn't a book available, but I do know that

for the capacitor: I = C*dV/dt
and for the resistor V = RI,

But "open circuit", does that mean that the circuit is equivalent with this image, see picture:

 

[gneill]

Yes, sadly the course I'm taking is horrible, and there really isn't a book available, but I do know that

for the capacitor: I = C*dV/dt
and for the resistor V = RI,

Yes, but you should also find expressions for I(t) , Q(t), and V(t) for charging and discharging the basic RC circuit configuration.

If they're not in your notes then a web search will turn up what you need.

But "open circuit", does that mean that the circuit is equivalent with this image, see picture:

Yes.

 

[johann1301h]

I found, using Kirchhoffs laws, the following: but I don't know how to go further

 

[johann1301h]

How do i find I (current) as function of time?

 

[gneill]

How do i find I (current) as function of time?

You would have to recognize that for a capacitor,
$$I_c = C \frac{dV_c}{dt}$$
and similarly,
$$V_c = \frac{1}{C} \int{I_c} \, dt$$
then solve the resulting differential equation(s).

It is much faster to recognize that for a DC driven RC circuit, all currents and potential differences will have the form of decaying or growing exponential functions ($A e^{t/\tau}$ or $A(1 - e^{t/\tau}$). Then it's a matter of determining the time constant $\tau$ for the circuit and finding the initial and steady state values for the quantities in question and writing the appropriate equations to fulfill those conditions.

Have you studied how to determine initial and steady state conditions for a circuit with capacitors?

 

[johann1301h]

I think I understand more now, I have to assume that I and V are functions of time, find a/the differential equation and solve it?

 

[johann1301h]

Have you studied how to determine initial and steady state conditions for a circuit with capacitors?

Well, I assume that there is no charge in the capacitor at t=0, is that what you mean?

 

[gneill]

Well, I assume that there is no charge in the capacitor at t=0, is that what you mean?

Yes, and how does it make the capacitor appear to the surrounding network at that instant of time?

When steady state is achieved, how much current does a capacitor draw or supply in the circuit? How then does the capacitor appear to the surrounding network at that time?

How can you use this information to find the initial and final values of voltages and currents?

 

[gneill]

I think I understand more now, I have to assume that I and V are functions of time, find a/the differential equation and solve it?

That is the "starting from the basics" approach, yes.

It's much quicker to already know what the solution is going to look like and then simply writing down the function of time.

 

[johann1301h]

At t = 0 i suppose all charged particles would move into the capacitor, and none would go through R1. And at the steady state it would be the other way around; the capacitor draws zero current (none can pass). And I guess it would appear as if the capacitor would be like an open circuit? I am a on to something?

 

[gneill]

At t = 0 i suppose all charged particles would move into the capacitor, and none would go through R1. And at the steady state it would be the other way around; the capacitor draws zero current (none can pass). And I guess it would appear as if the capacitor would be like an open circuit? I am a on to something?

You are definitely on to something.

So for the capacitor, can you tell me what the initial and final voltages will be?

 

[gneill]

Let's re-draw the circuit so that it's in a more familiar layout:

 

[johann1301h]

Since there are no charged particles in the capacitor at t=0, I guess the voltage V_c would be zero.

 

[johann1301h]

But also, because V_c = Q/C = 0/C = 0

 

[johann1301h]

For the final voltage I guess;

V_s - I₂R₂ - V_c = 0

V_c = I₂R₂ - V_s

 

[johann1301h]

But also;

V_s - I₂R₂ - I₁R₁ = 0

V_s = I₂R₂ + I₁R₁

But because of Kirchhoffs current law, I₁ = I₂

Which gives

V_s = I₂(R₂ + R₁)

Therefore

V_c = I₂R₂ - V_s = I₂R₂ - I₂(R₂ + R₁) = I₂R₁

V_c = I₂R₁?

 

[gneill]

To determine what the final potential across the capacitor will be, remove the capacitor from the circuit (it draw no current anyways). Then look at what remains of the circuit. There will be no time-varying values anywhere in the circuit so you can treat it just as you would any resistor network being driven by a DC source. Determine the potential between the points where the capacitor was removed.

 

[johann1301h]

Determine the potential between the points where the capacitor was removed.

That would be the voltage over R₁? Which is I₂R₁

 

[gneill]

That would be the voltage over R₁? Which is I₂R₁

Sure, but what is I₂? You should be able to find these values using only the given component variable names, no introduced unknown values.

 

[johann1301h]

l₂ = V_s/(R₁+R₂)

Giving

V_c = l₂R₁ = V_sR₁/(R₁+R₂)

 

[gneill]

Right! Now you have final "values" for the capacitor voltage and the currents i₁ and i₂.

Do the same for their initial values. To find initial values, take the capacitor voltage to be zero (replace the capacitor with a short circuit) and analyze the circuit.

 

[johann1301h]

I₁ = 0

and

I₂ = V_s/R₂ ?

 

[johann1301h]

But I still don't see how this can help me find I₁(t), I₂(t) and I_c(t)

 

[gneill]

I₁ = 0

and

I₂ = V_s/R₂ ?

Looks good. Let's see if we can't write an equation for one of the currents, say $i_1$.

We know that $i_1$ starts out at zero and ends up at $V_s/(R_1 + R_2)$. What form of exponential curve grows from 0 to some asymptotically approached final value? Hint, it looks like this:

 

[johann1301h]

I₂(t) = V_s/R₂(1-e^-t)

This is great, but I would never have guessed that the solution would be in this form, what kind of argumentation can be given for this?

 

[johann1301h]

Wait, I think I did something wrong...

 

[johann1301h]

I think I meant;

I₁(t) = V_s/(R₁ + R₂)(1-e^-t)

 

[gneill]

Yes, only there's one thing missing. The exponent needs a time constant.
$$e^{-\frac{t}{\tau}}$$

This is great, but I would never have guessed that the solution would be in this form, what kind of argumentation can be given for this?

Yes, it's the solution for the differential equation. As I mentioned before, ALL values that vary in an RC circuit (or an RL circuit) take the form of exponential growth or decay. You should be able to find the differential equation solved for the trivial RC circuit in your text, or failing that, just look up "RC circuit" on the web.

So about the time constant $\tau$. If you remove the capacitor from the circuit and suppress the voltage supply, what net resistance does the capacitor "see" at its terminal connection points?

 

[johann1301h]

Ok, i have a lot to digest here. One question though, are we not assuming that V_s is constant ?

 

[gneill]

Ok, i have a lot to digest here. One question though, are we not assuming that V_s is constant ?

Yes. It's referred to as being a battery in the problem statement.

 

[johann1301h]

Oh yes! Battery = constant V_s, I get it!

So about the time constant τ. If you remove the capacitor from the circuit and suppress the voltage supply, what net resistance does the capacitor "see" at its terminal connection points?

Do you mean to "remove" the capacitor when it is fully charged? And what du you mean by suppressing the voltage ?

 

[gneill]

Oh yes! Battery = constant V_s, I get it!
Do you mean to "remove" the capacitor when it is fully charged? And what du you mean by suppressing the voltage ?

It doesn't matter when you remove it. With the battery suppressed, the network will be dead anyways.

By "suppressed" I mean replaced with a short circuit. If it were a current source, you'd replace it with an open circuit. Have you not been introduced to Thevenin equivalents yet? Or circuit analysis by superposition?

 

[johann1301h]

Or circuit analysis by superposition?

If you mean by using complex numbers, briefly.

Have you not been introduced to Thevenin equivalents yet?

No, my university (University of Oslo) has a tendency to skim the surface of each subject. Its really sad!

From your sketch I can guess that R_eq = R₁

And therefore (perhaps) τ = R₁?

 

[johann1301h]

Not only from your sketch though, I get what you said here

what net resistance does the capacitor "see" at its terminal connection points?

 

[gneill]

If you mean by using complex numbers, briefly.

No, the superposition method of circuit analysis is where you suppress all the sources but one, analyze the resulting circuit to find the effect of the one operating source. Then do the same for each source in turn. When you're done, add up all the individual contributions. The method relies on the fact that circuits with only linear elements (like resistors, capacitors, inductors) behave as linear systems so that the contributions of each source add algebraically.

From your sketch I can guess that R_eq = R₁

And therefore (perhaps) τ = R₁?

Nope. How are $R_1$ and $R_2$ connected?

And the time constant will have units of time. So $\tau = R_{eq} C$

 

[johann1301h]

Yes, I see, the current would go through both R₁ and R₂...

 

[gneill]

Yes, I see, the current would go through both R₁ and R₂...

So how are they connected? In series or in parallel? Does the same current go through both (series connection) or do they take different currents (parallel connection)?

 

[johann1301h]

Using Kirchhoffs again

V_c = IR₁

and

V_c = IR₂

gives

2V_c = IR₁ + IR₂ =I(R₁ + R₂)

V_c = IR₁ + IR₂ =I(R₁ + R₂)/2

So it "sees" the average of R₁ and R₂?

 

[gneill]

No, you've made the assumption that the currents through both resistors would be the same $I$.

How do you "add" resistors in parallel? In series? Have you done any circuit simplification exorcises where you have to combine and reduce the number of resistors?

 

[johann1301h]

R_eq = R₁R₂/(R₁ + R₂)

 

[johann1301h]

τ = C*R1R2/(R1 + R2) ?

 

[gneill]

R_eq = R₁R₂/(R₁ + R₂)

Yes! That's the resistance that the capacitor "sees" when it's in-circuit.

So the time constant for this circuit is $\tau = R_{eq} C$. It will apply to every exponential function involved in this circuit.

 

[johann1301h]

I see, I will try to find I₂ as well!

 

[gneill]

So, can you now do the same thing for the capacitor voltage? You know it starts at zero and goes up to $V_s \frac{R_1}{R_1 + R_2}$.

 

[gneill]

I see, I will try to find I₂ as well!

Excellent. It would be great if you could do that. It'll be a bit more tricky (but not much!) since it doesn't start or end at zero values, so there will be a constant offset to add.

 

[gneill]

No, my university (University of Oslo) has a tendency to skim the surface of each subject. Its really sad!

I am curious, if and if you don't mind and have the time, could you tell me what program you are in and in what course in particular this question was posed? The reason I ask is that it seems that you've been pushed into the deep end of the circuit pool without being given the right background information to survive!