Physicslearner500039
- 124
- 6
- Homework Statement
- In if coil 2 is turned so that its axis is vertical, does the mutual inductance increase or decrease? Explain.
- Relevant Equations
- emf = ##\frac {-N_{2} {d\phi}_{B2}} {dt}## ## M_{21} = \frac {{N_2}{\phi}_{B2}} {i_1}##
emf = ##\frac {-N_{2} {d\phi}_{B2}} {dt}## ## M_{21} = \frac {{N_2}{\phi}_{B2}} {i_1}## are the equations
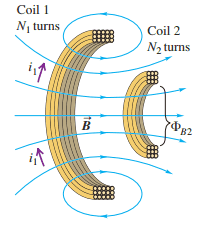
This is the original position, now the coil 2 is moved so the axis is perpendicular. The flux ##{\phi}_{B2}## due to i1 is the amount of flux cutting the coil 2 due to change in current i1. My answer is 0, since no flux cuts the Coil 2 in 90 degrees position. Is it correct? My main confusion is with respect to the area of the coil. How to consider it? i do not see the coil 2 as closed circuit it is open loop. So, what will be the area. Please advise.
Note: One another problem is i cannot preview the Homework statement and the Relevant Equations section. I have a workaround for the equations section, but still not sure if latex symbols work for the Homework statement. Please advise.
This is the original position, now the coil 2 is moved so the axis is perpendicular. The flux ##{\phi}_{B2}## due to i1 is the amount of flux cutting the coil 2 due to change in current i1. My answer is 0, since no flux cuts the Coil 2 in 90 degrees position. Is it correct? My main confusion is with respect to the area of the coil. How to consider it? i do not see the coil 2 as closed circuit it is open loop. So, what will be the area. Please advise.
Note: One another problem is i cannot preview the Homework statement and the Relevant Equations section. I have a workaround for the equations section, but still not sure if latex symbols work for the Homework statement. Please advise.