Ramtin123
- 22
- 0
I am trying to compute the cross-section for the diagram below with a divergent triangle loop:
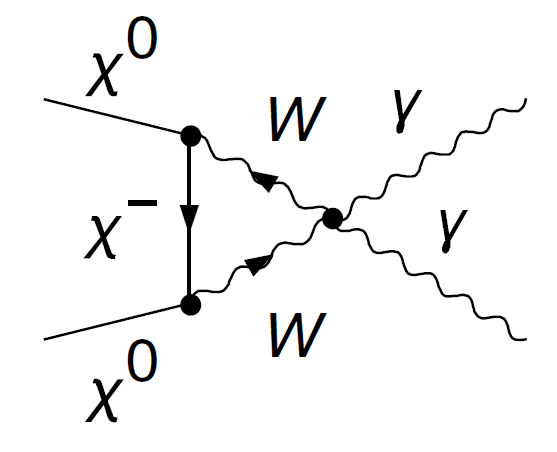
where ##X^0## and ##X^-## are some fermions with zero and negative charge respectively. I am interested in low energy limits, so you can consider W-propagator as ##\frac {i\eta_{\mu\nu}} {M_w^2}##.
When computing the amplitude, you end of with an integration of the form:
$$ \int \frac {k_\mu \gamma^\mu +m_-} {k^2 -m_-^2} \frac {d^4 k} {(2\pi)^4} $$
where ##m_-## is mass of ##X^-##.
Any ideas how to find the amplitude in terms of kinematic parameters, masses etc?
where ##X^0## and ##X^-## are some fermions with zero and negative charge respectively. I am interested in low energy limits, so you can consider W-propagator as ##\frac {i\eta_{\mu\nu}} {M_w^2}##.
When computing the amplitude, you end of with an integration of the form:
$$ \int \frac {k_\mu \gamma^\mu +m_-} {k^2 -m_-^2} \frac {d^4 k} {(2\pi)^4} $$
where ##m_-## is mass of ##X^-##.
Any ideas how to find the amplitude in terms of kinematic parameters, masses etc?