Condition of the charge density of atom

[Pushoam]

Homework Statement

Homework Equations

The Attempt at a Solution

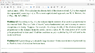
$\rho = b r \\E =\frac { k r^2} {4ε_0} \\ p ∝ E^a \\E \left ( r=d \right ) = \frac { k d^2} {4ε_0} \\ p = q d \\ d ∝ d^{2a} \\a = ½ \\p ∝ √E$

PART B

$\rho ∝ r^n \\E ∝r^{n+1} \\ p ∝ E^a \\d ∝d ^{{n+1}a} \\$ For eq. 4.1 to hold, $a = \frac 1 { n+1} =1 \\ n = 0$
So, rho should be constant.

 

[TSny]

OK. I think your answers are correct. Note that you are dealing with two different electric fields: the applied electric field and the field of the negative charge distribution. It would be nice if you explained why you didn't bother to distinquish between these fields in your calculation.

Can you give a more general proof for part B that does not assume that $\rho(r)$ varies as $r$ to some power?

 

[Pushoam]

It would be nice if you explained why you didn't bother to distinquish between these fields in your calculation.

In equilibrium, net force acting on the nucleus ## \vec F_{net} = q\left ( \vec E_{app.} + \vec E_ {ne. ch. dis. }\right ) = 0 \\ | \vec E_{app.}| = | \vec E_ {ne. ch. dis. }|

Can you give a more general proof for part B that does not assume that ρ(r)ρ(r)\rho(r) varies as rrr to some power?

Using Taylor's expansion, I can write $\rho \left ( r \right)$ as a polynomial function of r.
So, $\rho \left (r \right ) = Ar^n + B r^{n - 1} +... + Nr^0$
So, the same procedure will give me $\\d ∝ Ad ^{\{{n+1}\}a} + B d^na + Cd ^{\{{n-1}\}a}+... + \ln r$
Now, what to do?

 

[TSny]

In equilibrium, net force acting on the nucleus $\vec F_{net} = q\left ( \vec E_{app.} + \vec E_ {ne. ch. dis. }\right ) = 0 \\ | \vec E_{app.}| = | \vec E_ {ne. ch. dis. }$

Yes.

Using Taylor's expansion, I can write $\rho \left ( r \right)$ as a polynomial function of r.
So, $\rho \left (r \right ) = Ar^n + B r^{n - 1} +... + Nr^0$
So, the same procedure will give me $\\d ∝ Ad ^{\{{n+1}\}a} + B d^na + Cd ^{\{{n-1}\}a}+... + \ln r$
Now, what to do?

I don't think you need to consider a Taylor expansion. What if you set up Gauss' law for a spherical surface of radius $r$ with $r<R$ and an arbitrary $\rho(r)$?

 

[Pushoam]

I don't think you need to consider a Taylor expansion. What if you set up Gauss' law for a spherical surface of radius r with r<R and an arbitrary ρ(r)?

p = qr = α E

E = $\frac 1 {4 \pi ε_0 r^2} \int_0 ^r 4 \pi \rho \left (r \right ) r^2 d\, r$
qr = α $\frac 1 {4 \pi ε_0 r^2} \int_0 ^r 4 \pi \rho \left (r \right ) r^2 d\, r$

Dimensional analysis gives constant ρ as a possible answer.
But, I can't prove that ρ must be constant. Is there any uniqueness theorem to help prove so?

 

[TSny]

qr = α $\frac 1 {4 \pi ε_0 r^2} \int_0 ^r 4 \pi \rho \left (r \right ) r^2 d\, r$

Bring the denominator $4 \pi ε_0 r^2$ over to the left side. Then take the derivative of both sides with respect to r.

 

[Pushoam]

Bring the denominator$4 \pi ε_0 r^2$over to the left side. Then take the derivative of both sides with respect to r.

O.K. So, for proving that $\rho \left (r \right )$ is constant, I have to bring $\rho \left (r \right )$ out of the integration.
And this could be done by differentiating both sides wrt r. I never had this idea before. Thanks for giving this insight.

$qr =\alpha \frac 1 {4 \pi ε_0 r^2} \int_0 ^r 4 \pi \rho \left (r \right ) r^2 d\, r$
$r^3 = C \int_0 ^r \rho \left (r \right ) r^2 d\, r$
Differentiating both sides wrt r,
$r^2 = C' \rho \left (r \right ) r^2 \\ \rho \left (r \right ) = C"$
Where C, C' and C" are appropriate constants.

While I have used here,
$\frac {d \int_0 ^r f \left (r \right ) d\, r} {dr} = f\left (r \right )$
Proof:
$\int_0 ^r f \left (r \right ) d\, r = F \left (r \right ) + F \left (0 \right )$
Since integration and differentiation are inverse operation of each other,
$\frac {d\{F \left (r \right ) + F \left (0 \right )\} } {dr} = f \left (r \right ) \\ \frac {d \int_0 ^r f \left (r \right ) d\, r } {dr} = f \left (r \right )$

 

[Pushoam]

Solution of the 2nd part of this question gives : For eqn. 4.1 to hold true in the weak field limit , the negative charge density of the atom must be constant. This means that the electron cloud should be uniformly distributed.

Now , in solving the following problem

where the charge density is not constant, I used the eqn. 4.1.
So, does this mean that I solved it wrong?

 

[TSny]

Solution of the 2nd part of this question gives : For eqn. 4.1 to hold true in the weak field limit , the negative charge density of the atom must be constant. This means that the electron cloud should be uniformly distributed.

Now , in solving the following problem
View attachment 208501

where the charge density is not constant, I used the eqn. 4.1.
So, does this mean that I solved it wrong?

No, you probably solved it correctly. For 4.1 to hold (to a good approximation), you only need the electron cloud to be approximately uniform in the vicinity of the nucleus since the displacement of the nucleus relative to the center of the cloud will be very small in the weak field limit. Thus, you can use $e^{-x} \approx 1-x \approx 1$ for small x for the hydrogen atom cloud. So, you can treat the cloud as uniform in the neighborhood of the nucleus. Therefore, you can use 4.1.

 

[Pushoam]

Thus, you can use $e^{-x} \approx 1-x \approx 1$ for small x for the hydrogen atom cloud.

Under this approximation i.e. $e^{-x} \approx 1-x \approx 1$ , the answer to the problem 4.2 is $4 \pi ε_0 a^3$.
While the answer given in the solution of the book is $3 \pi ε_0 a^3$. I am attaching the solution to the problem for both the cases i.e. uniform and non- uniform charge density.

 

[TSny]

I don't see the need to go through the tedious calculation shown in the solution. If you approximate the exponential by 1, then the charge density near the nucleus is approximately uniform, $\rho = \frac{q}{\pi a^3}$. That will yield $\alpha = 3 \pi a^3 \varepsilon_0$.

 

[Pushoam]

I don't see the need to go through the tedious calculation shown in the solution. If you approximate the exponential by 1, then the charge density near the nucleus is approximately uniform, $\rho = \frac{q}{\pi a^3}$. That will yield $\alpha = 3 \pi a^3 \varepsilon_0$.

Oh yeah! I got my mistake. Here, the total charge is $\frac 3 4 q$ instead of q.

Thank you.

 

[TSny]

OK, good.