mgmt113
- 3
- 0
Homework Statement
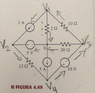
The problem states: Determine the voltage labeled v in the following circuit: https://ibb.co/hz0Q37
The variable is the voltage across the 2 ohm resistor. The ground I chose for this example is located in the center of the circuit.
Homework Equations
V=IR I guess.
The Attempt at a Solution
I have a huge confusion regarding current directions. How come the textbook says that you can choose any current direction you want as long as you're consistent, but when I choose them to be a certain way trying to be consistent, I get the wrong answer? When I check solved problems, they assume current directions and I would have not gotten the same answers if I chose my directions. So, can you really choose the directions you want, and am I missing something important?
These are the equations I got. I got all the terms on one side to avoid confusion. If the current is entering the node, then I assign it a negative sign, if it's leaving the node, it stays positive.
For Node 1 (the one in the uppermost part of the circuit)
1 + (V3-V1)/10 + V1/2 = 0
For Supernode 2-4
-1 + (V2-V4)/12 - V3/20 + 5 -V1/2 = 0
For Supernode 3-4
V3/20 + (V1-V3)/10 -5 + (V4-V2)/12 = 0
The answer for V1 that I get is -0.5 V, however the solution manual says it's 1.7 V.
Are the directions I posted on the image right? If not, why? And is there an strategy to avoid getting confused at directions?
Thank you very much for your help. I really appreciate it.
Attachments
Last edited by a moderator: