Confused about Polarity of Induced EMF (Lenz Law)

[nyxynyx]

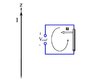
Hello, I am currently working through Faraday's Law and I am confused when my two textbooks don't explain how they set the polarity of V_{emf}, particularly when they say "the sign convention for V_{emf} is arbitrary in that it depends on the assumed direction for dS". How is the polarity related to dS?

The formula I am using is v_{emf} = - \int_c \vec{B}\cdot d\vec{S} = \oint_c \vec{E}\cdot d\vec{L}

Here's a diagram that you can try explaining it from.

Thanks!

 

[Doc Al]

For one thing, that equation is incorrect. http://hyperphysics.phy-astr.gsu.edu/Hbase/electric/farlaw.html" states how the induced EMF relates to the rate of change of the magnetic flux (\Phi):

{EMF} = - d\Phi/dt

The polarity of the EMF (the meaning of the minus sign) is given by http://hyperphysics.phy-astr.gsu.edu/Hbase/electric/farlaw.html#c2".

 

[nyxynyx]

Oops i left out the time differential. Can anyone explain what my textbook is saying?

 

[Doc Al]

What they are trying to tell you is that the orientation of the surface determines the direction of the line integral. Imagine a circle (which we'll be finding the flux through) drawn on the x-y plane at z = 0 . If we arbitrarily choose +z as the direction of the surface element (dS) that means the line integral will go counter-clockwise when viewed from the +z axis looking down. And if we choose the opposite orientation, the line integral will go clockwise when viewed from +z.

So if we've chosen an orientation such that the line integral goes clockwise, a negative EMF means that the EMF is oriented counter-clockwise.

Make sense?

 

[Phrak]

Doc Al. Lenz's Law in my text reads more like a hastily scribbled perscription than single law. First there's a given flux that yields the chirility of the EMF. Then an (implied) inducted current. Then the induced current is said to product a magnetic field that opposes the induced flux.

 

[Doc Al]

Doc Al. Lenz's Law in my text reads more like a hastily scribbled perscription than single law. First there's a given flux that yields the chirility of the EMF. Then an (implied) inducted current. Then the induced current is said to product a magnetic field that opposes the induced flux.

Lenz's law can be considered part of Faraday's law--the part that helps you determine the direction of the induced EMF (the negative sign in Faraday's law). It's a consequence of energy conservation. Not sure what you mean by calling it "hastily scribbled".

 

[Phrak]

Lenz's law can be considered part of Faraday's law--the part that helps you determine the direction of the induced EMF (the negative sign in Faraday's law). It's a consequence of energy conservation. Not sure what you mean by calling it "hastily scribbled".

Well, perhaps "hasilt scribbled" is overly critical. But what I'm given are really three laws rather than one. If I break them down into my own numbering, Lenz1 determines the direction of EMF as you say.

The secone one (Lenz2) says that there could be a current as a result of the EMF, which seems to be a already obtained from Lorentz law.

Lenz3 says that an induced current generates an additional magnetic flux in opposition to the impressed flux. It's the result of two handedness operations, so I don't think it is really dependent upon Lenz1 anymore; the induced flux acts to impose the impressed flux no matter what handedness you give the coordinate system. Though my text later presents self inductance as a result of Lenz3, I'm skeptical that Lenz3 is an independent axiom that isn't inherent in Faraday's Law.