righteous818
- 7
- 0
I have attachted the question as a picture:
my first attempt i calculated the voltage through the auxillary circuit to be 10V but i am confused of where the 0.5 A plays in this part, then i used nodal analysis to find the voltage input to the amplifier but up to that point i am confused of how to proceed, am i working the question through the right steps or am i missing something
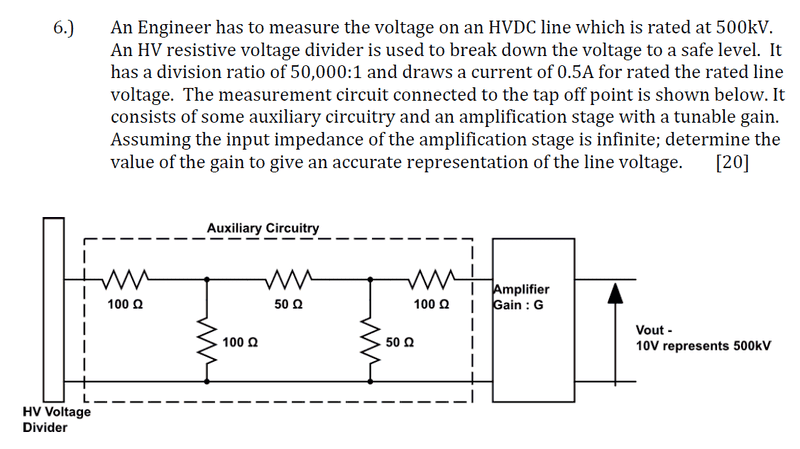
my first attempt i calculated the voltage through the auxillary circuit to be 10V but i am confused of where the 0.5 A plays in this part, then i used nodal analysis to find the voltage input to the amplifier but up to that point i am confused of how to proceed, am i working the question through the right steps or am i missing something