Coriolis Force on a Rotating and Inclined Plane

[AGP]

Homework Statement

I'm having a lot of trouble figuring this one out:

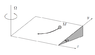
Study the trajectory of a free particle of mass M released from a state of rest on a
rotating, sloping, rigid plane. The angular rotation rate is Omega, and the
angle formed by the plane with the horizontal is alpha. Friction and the centrifugal force
are negligible. What is the maximum speed acquired by the particle, and what is its
maximum downhill displacement?

I attached a figure which shows what's going on, for clarification.

Homework Equations

The relation between absolute and relative velocities is as follows:

U = u - OMEGA*y
V = v + OMEGA*x

where U and V are the absolute velocities in the absolute X and Y directions, respectively; u and v denote the velocities in the rotating x and y frames. For unforced motion, the above simplify to:

u - OMEGA*y = 0
v + OMEGA*x = 0

The Attempt at a Solution

I'm having a lot of trouble accounting for the fact that the y-axis is not orthogonal to either the x-axis or the axis of rotation. I've tried accounting for that by defining a new y-axis, y' which is orthogonal, but the math is blowing up. The motion should be forced only by gravity, but I'm having no luck with the following:

-M*g*sin(alpha) = M*du/dt - fv

It works out via system of linear ordinary equations (by my math) to:

d^2v/dt^2 + f^2v +g*f*sin(alpha) = 0

Which seems far more complicated that it should at this level. Thanks in advance for any help!

 

[mark726]

Thank you for your question. The problem you are trying to solve involves the study of a free particle on a rotating, sloping, rigid plane. In order to solve this problem, we need to take into account the forces acting on the particle and use the appropriate equations to find the maximum speed acquired and the maximum downhill displacement.

First, let's consider the forces acting on the particle. As stated in the problem, we can neglect friction and the centrifugal force, leaving only the force of gravity acting on the particle. This force can be decomposed into two components: one parallel to the slope of the plane, and one perpendicular to the slope.

Next, we need to define our coordinate system. Since the plane is rotating, it is convenient to use a rotating coordinate system with the origin at the particle's initial position. Let's call this coordinate system x' and y', with the x' axis aligned with the slope of the plane and the y' axis perpendicular to it.

Using the equations provided in the problem, we can relate the velocities in the rotating coordinate system to the absolute velocities. However, since the y' axis is not orthogonal to the x' axis or the axis of rotation, we need to account for this in our equations. This can be done by introducing a rotation matrix that relates the rotating coordinate system to the absolute coordinate system.

With this in mind, we can write the equations of motion for the particle as follows:

m*d^2x'/dt^2 = m*g*sin(alpha)*cos(Omega*t) - m*f*v*cos(Omega*t)
m*d^2y'/dt^2 = m*g*cos(alpha) - m*f*v*sin(Omega*t)

where m is the mass of the particle, v is the speed of the particle, f is a constant related to the slope of the plane, and t is time.

To solve for the maximum speed and maximum downhill displacement, we can use the equations of motion to set up a system of differential equations and solve them numerically. Alternatively, we can use energy conservation to find the maximum speed and use the equations of motion to find the maximum downhill displacement.

I hope this helps in solving your problem. If you have any further questions or need clarification, please don't hesitate to ask. Good luck with your studies!