Current flow direction in "infinite" cube of 1ohm resistors

[BiGyElLoWhAt]

Homework Statement

Write a program to find the equivalent resistance between two opposite corners within a grid of "infinite size" with resistors between each point.
So basically we have an infinite cube made up of cubes with 1 ohm resistors between each node.

Homework Equations

Kirkoff's laws

The Attempt at a Solution

Really what I'm having problems with is defining the direction of the current in a way that is consistent and allows every point a path from V+ to V-=0

I'm using a 1001x1001x1001 array that will hold the coefficients for each kirkoffs current law at each point. I am setting 500,500, 500 = V+ and 501,501,501 = 0 V (so it's symmetric about the central cube of resistors).

What I'm doing so far,I have k=500 and drew a plane and sketched out the current paths.
I have for the current direction: (it won't let me put pseudocode as the language)

#for the i direction of current
if j<= 500
    if i < 500
        I = -i # (meaning I take V(i+1,j,500) to be higher V than V(i,j,500)
    if i >500
        I = + i #(Vi > Vi+1)
    if i=500
        I = -+ i # (V(500,j,500) > V(501,j,500) && V(499,j,500) (I is - i to the left and + i to the right)
if j = 501
    if i < 501
       I = + i
    if i = 501
       I = +-i #V( 501,501,500) < all adjacent points except for V(501,501,501) ) (I is +i to the left and -i to the right)
    if i > 501
        I = -i
if j > 501
   I = +i

I'm measuring the equivalent resistance between 500,500,500 and 501,501,501

This feels like a bit overkill, so my question, is there a better way to write this?
Really all I need is for every point to have a complete path to 501,501,501 and a complete path from 500,500,500 to that point. Additionally, I need 500,500,500 to send out current in all directions and 501,501,501 to take current from all directions.

In the picture, the arrows indicate the current flow, the solid circle indicates that the point is V+ and the empty circle indicates that V- = 0 is in the adjacent plane.

***Edit***
I changed the current flow direction from 499,501,500 -> 500,502,500 to be in the opposite direction so that I have less cases to handle for the j direction.
***Edit again***
Crap, I think I need a 6d array, 3d for the point and 3d for the coefficients...
So I'll basically have $V_{ijklmn}V^{lmn} = B_{ijk}$
There's got to be something stupid I'm doing.
***Edit numero tres***
So with the 6d array, the biggest I can make it on my pc is 17^6, otherwise I get a memory error. I might be able to make it a couple points larger if I close everything out, but I don't think 17^3 cube is large enough to get a reasonable approximation. Any suggestions?
**4**
I just allocated 16Gb to a paging file, and now I can go to 19^6 lol... 21 still gives me a memory error, though.
**5**
So I'm not using any quantity of my memory. A 17^3 array of zeros is about 184 Mb. (193100552 bytes)/(1024^2)

 

[mfb]

Kirchhoff.

You won't find an analytic solution with a program, so you have to use a numerical simulation. In this case you can simplify the program a lot with an iterative approach.

In equilibrium, can you find the voltage at a node (apart from the two fixed ones) if you know the voltages of the nodes around it? Just use some starting grid voltages, then update voltages iteratively.

 

[emcsquared]

*Not an expert*

They don't mean 2 opposite corners of the entire grid do they? That would be a very different problem.

The current between any 2 nearby resistors would effectively be zero wouldn't it?

 

[mfb]

They don't mean 2 opposite corners of the entire grid do they? That would be a very different problem.

I was wondering the same. Once the program is set up it does not make a large difference, however.

 

[BiGyElLoWhAt]

No, I'm trying to find the current out of either 500,500,500 or into 501,501,501 (should be same magnitude). I'm trying to find the equivalent resistance between those two points. Why can't I find an analytical solution? Shouldn't I be able to set up Kirkoff's current equations for each point as a function of the adjacent points and then use linalg.solve (or whatever it is) to diagonalize my matrix along with my solutions matrix? There's a function that takes two matrices (A,B) and solves Ax=B in the linalg library in python.

 

[Tom.G]

In the similar problems I've seen, reference to a 'grid' has meant a 2-D grid, not 3-D. Verify with instructor maybe?

 

[The Electrician]

Have a look at these: https://sites.google.com/site/resistorgrid/

http://www.mathpages.com/home/kmath668/kmath668.htm

 

[BiGyElLoWhAt]

It's definitely 3d. It explicitly said a cube of resistors.
"Assume you have an infinite cubic grid of resistors, each of 1 ohm as shown below. Please program so that you can figure out the equivalent resistance between one of the body diagonal, as marked below"

Doesn't really do much good, since I don't have the image to upload.

 

[BiGyElLoWhAt]

Anyway, is there anyway to do this without resorting to 6d matrices? I am having trouble seeing it if there is. What I'm thinking is that I need a 3d matrix for each point for the kirkoff's current equation for that point (which would be a 3d function). Maybe if I could write my own solver, I could get away with something smaller range-wise. I only need the adjacent points in the equation, and nothing further away than that, so really I should be able to get away with 6d, as in [L,L,L,2,2,2]. All of the values depending on the point in question cancel out (at least for i,j,k <(L-1)/2 ). I would assume that it will happen everywhere except for my 2 fixed points. Some of the students asked about how to do it, and this was the method he suggested using.

I'm not sure how I could use the 2,2,2 effectively, though. They would reference different vectors for different values of i,j,k. So i,j,k = 1 would be (1,1,1,[1,-1],[1,-1],[1,-1]) but the vectors in the l,m,n matrices would represent [V(i+1,j,k),- V(i-1,j,k)] , [V(i,j-1,k),- V(i,j+1,k)] , [V(i,j,k+1),- V(i,j,k-1)] for i,j,k <(L-1)/2

 

[mfb]

Your grid in the problem statement is infinite. Even if you can find an analytic solution for the 1001³ cube (which is theoretically possible), that is not an analytic solution for the full problem.

Did you find the equation I was mentioning in post 2? It gives you a single, easy equation for each grid point.

 

[BiGyElLoWhAt]

I didn't. Also, we're only supposed to be getting an approximation.

Are you suggesting that I use the symmetry of the cube to draw equipotential lines and work my way out from the two fixed points?

 

[mfb]

Also, we're only supposed to be getting an approximation.

I know. So why don't you try to solve massive equation systems exactly?

Are you suggesting that I use the symmetry of the cube to draw equipotential lines and work my way out from the two fixed points?

No, that won't help, you just know one equipotential area.

I suggest to do what I suggested in post 2. Once you have that, the problem should be easy. In 2D, it is literally just one minute of work with Excel (old example), in 3D it is a few minutes of coding and a bit more for running (I would limit the grid to something like (101)³ entries for reasonable computing times).

 

[BiGyElLoWhAt]

Ok so I got it finished. I did it both ways, the averaging method, and also with linalg.tensorsolve. The averaging gives a result of about .24 ohms with 150 averages (about .23 with 50) and with the tensor algebra, I get R equivalent of about .21.

Spoiler: Averaging

from __future__ import division
from numpy import zeros

l = 21
V = zeros((l,l,l))def average(i,j,k):
   
    total = 0
    if i != 0 and i!= l-1:
       
        if j!= 0 and j!=l-1:
           
            if k!=0 and k!= l-1:
               
                total = V[i+1,j,k] + V[i-1,j,k] + V[i,j+1,k] + V[i,j-1,k] + V[i,j,k+1]+ V[i,j,k-1]
            if k == 0 :
               
                total = V[i+1,j,k] + V[i-1,j,k] + V[i,j+1,k] + V[i,j-1,k] + V[i,j,k+1]
            if k == l-1:
               
                total = V[i+1,j,k] + V[i-1,j,k] + V[i,j+1,k] + V[i,j-1,k] + V[i,j,k-1]
        if j == 0:
           
            if k!= 0 and k!= l-1:
               
                total = V[i+1,j,k] + V[i-1,j,k] + V[i,j+1,k] + V[i,j,k+1]+ V[i,j,k-1]
            if k == 0:
               
                total = V[i+1,j,k] + V[i-1,j,k] + V[i,j+1,k] +  V[i,j,k+1]
            if k == l-1:
               
                total = V[i+1,j,k] + V[i-1,j,k] + V[i,j+1,k]  + V[i,j,k-1]
        if j == l-1:
           
            if k!= 0 and k!=l-1:
                total = V[i+1,j,k] + V[i-1,j,k] + V[i,j-1,k] + V[i,j,k+1]+ V[i,j,k-1]
            if k == 0:
               
                total = V[i+1,j,k] + V[i-1,j,k] + V[i,j-1,k] + V[i,j,k+1]
            if k == l-1:
               
                total = V[i+1,j,k] + V[i-1,j,k] +  V[i,j-1,k] +  V[i,j,k-1]
    if i == 0:
       
        if j!= 0 and j!=l-1:
           
            if k!=0 and k!= l-1:
               
                total = V[i+1,j,k] +  V[i,j+1,k] + V[i,j-1,k] + V[i,j,k+1]+ V[i,j,k-1]
            if k == 0 :
               
                total = V[i+1,j,k] + V[i,j+1,k] + V[i,j-1,k] + V[i,j,k+1]
            if k == l-1:
               
                total = V[i+1,j,k] + V[i,j+1,k] + V[i,j-1,k] + V[i,j,k-1]
        if j == 0:
           
            if k!= 0 and k!= l-1:
               
                total = V[i+1,j,k] +  V[i,j+1,k] + V[i,j,k+1]+ V[i,j,k-1]
            if k == 0:
               
                total = V[i+1,j,k] + V[i,j+1,k] +  V[i,j,k+1]
            if k == l-1:
               
                total = V[i+1,j,k] +  V[i,j+1,k]  + V[i,j,k-1]
        if j == l-1:
           
            if k!= 0 and k!=l-1:
               
                total = V[i+1,j,k] +  V[i,j-1,k] + V[i,j,k+1]+ V[i,j,k-1]
            if k == 0:
               
                total = V[i+1,j,k] +  V[i,j-1,k] + V[i,j,k+1]
            if k == l-1:
               
                total = V[i+1,j,k] +  V[i,j-1,k] +  V[i,j,k-1]
    if i == l:
       
        if j!= 0 and j!=l-1:
           
            if k!=0 and k!= l-1:
               
                total =  V[i-1,j,k] + V[i,j+1,k] + V[i,j-1,k] + V[i,j,k+1]+ V[i,j,k-1]
            if k == 0 :
               
                total =  V[i-1,j,k] + V[i,j+1,k] + V[i,j-1,k] + V[i,j,k+1]
            if k == l-1:
               
                total =  V[i-1,j,k] + V[i,j+1,k] + V[i,j-1,k] + V[i,j,k-1]
        if j == 0:
           
            if k!= 0 and k!= l-1:
               
                total =  V[i-1,j,k] + V[i,j+1,k] + V[i,j,k+1]+ V[i,j,k-1]
            if k == 0:
               
                total =  V[i-1,j,k] + V[i,j+1,k] +  V[i,j,k+1]
            if k == l-1:
               
                total =  V[i-1,j,k] + V[i,j+1,k]  + V[i,j,k-1]
        if j == l-1:
           
            if k!= 0 and k!=l-1:
                total =  V[i-1,j,k] + V[i,j-1,k] + V[i,j,k+1]+ V[i,j,k-1]
            if k == 0:
               
                total =  V[i-1,j,k] + V[i,j-1,k] + V[i,j,k+1]
            if k == l-1:
               
                total =  V[i-1,j,k] +  V[i,j-1,k] +  V[i,j,k-1]
       
           
   
   
   
    avg = total/6
    return avg
   
V[(l-1)/2,(l-1)/2,(l-1)/2] = 5
ii = 0
while ii < 150:
    for i in range(l):
        for j in range(l):
            for k in range(l):
                if i != (l-1)/2 or j != (l-1)/2 or k != (l-1)/2:
                    if i != (l+1)/2 or j != (l+1)/2 or k != (l+1)/2:
                        V[i,j,k] = average(i,j,k)
               
                elif all(x == (l-1)/2 for x in (i,j,k)):
                    V[i,j,k] = 5
                elif all(x == (l+1)/2 for x in (i,j,k)):
                    V[i,j,k] = 0
               

    ii+=1

i = (l-1)/2
j = (l-1)/2
k = (l-1)/2               
#print(V[i+1,j,k] , V[i-1,j,k] , V[i,j+1,k] , V[i,j-1,k] , V[i,j,k+1], V[i,j,k-1])

R=1
R_equivalent = V[i,j,k]/((6*V[i,j,k] - (V[i+1,j,k] + V[i-1,j,k] + V[i,j+1,k] + V[i,j-1,k] + V[i,j,k+1]+ V[i,j,k-1]))/R)
print("Equivalent Resistance is : ", R_equivalent)

Spoiler: Tensor Algebra

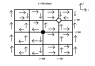
from __future__ import division
from numpy import zeros, linalg
#from pylab import nbytes
#import numpy

l = 3 # needs to be odd
V = zeros((l,l,l,l,l,l)) #voltage coeff at each point w.r.t ground
R = 1 #resistance
A = zeros((l,l,l)) #Solutions to the voltage equation i.e. a_ijk V^i = A_jk

def FillMatrix(i,j,k):   #Kirkoff's Current Law
    if i != 0 and i != l-1:
        if j != 0 and j != l-1:
            if k!= 0 and k!= l-1:
                V[i,j,k,i+1,j,k] = 1
                V[i,j,k,i,j+1,k] = 1
                V[i,j,k,i,j,k+1] = 1
                V[i,j,k,i-1,j,k] = 1
                V[i,j,k,i,j-1,k] = 1
                V[i,j,k,i,j,k-1] = 1
                V[i,j,k,i,j,k] = -6
                A[i,j,k]=0
            if k == 0:
                V[i,j,k,i+1,j,k] = 1
                V[i,j,k,i,j+1,k] = 1
                V[i,j,k,i,j,k+1] = 1
                V[i,j,k,i-1,j,k] = 1
                V[i,j,k,i,j-1,k] = 1
                #V(i,j,k,i,j,k-1) = -1
                V[i,j,k,i,j,k] = -5
                A[i,j,k]=0
            if k == l-1:
                V[i,j,k,i+1,j,k] = 1
                V[i,j,k,i,j+1,k] = 1
                #V(i,j,k,i,j,k+1) = 1
                V[i,j,k,i-1,j,k] = 1
                V[i,j,k,i,j-1,k] = 1
                V[i,j,k,i,j,k-1] = 1
                V[i,j,k,i,j,k] = -5
                A[i,j,k]=0
        if j == 0 :
            if k != 0 and k != l-1:
                V[i,j,k,i+1,j,k] = 1
                V[i,j,k,i,j+1,k] = 1
                V[i,j,k,i,j,k+1] = 1
                V[i,j,k,i-1,j,k] = 1
                #V(i,j,k,i,j-1,k) = -1
                V[i,j,k,i,j,k-1] = 1
                V[i,j,k,i,j,k] = -5
                A[i,j,k]=0            
            if k == 0:
                V[i,j,k,i+1,j,k] = 1
                V[i,j,k,i,j+1,k] = 1
                V[i,j,k,i,j,k+1] = 1
                V[i,j,k,i-1,j,k] = 1
               # V(i,j,k,i,j-1,k) = -1
               # V(i,j,k,i,j,k-1) = -1
                V[i,j,k,i,j,k] = -4
                A[i,j,k]=0
            if k ==l-1:
                V[i,j,k,i+1,j,k] = 1
                V[i,j,k,i,j+1,k] = 1
                #V(i,j,k,i,j,k+1) = 1
                V[i,j,k,i-1,j,k] = 1
                #V(i,j,k,i,j-1,k) = -1
                V[i,j,k,i,j,k-1] = 1
                V[i,j,k,i,j,k] = -4
                A[i,j,k]=0
        if j == l-1:
            if k != 0 and k != l-1:
                V[i,j,k,i+1,j,k] = 1
                #V(i,j,k,i,j+1,k) = 1
                V[i,j,k,i,j,k+1] = 1
                V[i,j,k,i-1,j,k] = 1
                V[i,j,k,i,j-1,k] = 1
                V[i,j,k,i,j,k-1] = 1
                V[i,j,k,i,j,k] = -5
                A[i,j,k]=0            
            if k == 0:
                V[i,j,k,i+1,j,k] = 1
                #V(i,j,k,i,j+1,k) = 1
                V[i,j,k,i,j,k+1] = 1
                V[i,j,k,i-1,j,k] = 1
                V[i,j,k,i,j-1,k] = 1
               # V(i,j,k,i,j,k-1) = -1
                V[i,j,k,i,j,k] = -4
                A[i,j,k]=0
            if k ==l-1:
                V[i,j,k,i+1,j,k] = 1
                #V(i,j,k,i,j+1,k) = 1
                #V(i,j,k,i,j,k+1) = 1
                V[i,j,k,i-1,j,k] = 1
                V[i,j,k,i,j-1,k] = 1
                V[i,j,k,i,j,k-1] = 1
                V[i,j,k,i,j,k] = -4
                A[i,j,k]=0           
    if i == 0:
        if j != 0 and j != l-1:
            if k != 0 and k!= l-1:
                V[i,j,k,i+1,j,k] = 1
                V[i,j,k,i,j+1,k] = 1
                V[i,j,k,i,j,k+1] = 1
                #V(i,j,k,i-1,j,k) = -1
                V[i,j,k,i,j-1,k] = 1
                V[i,j,k,i,j,k-1] = 1
                V[i,j,k,i,j,k] = -5
                A[i,j,k]=0
            if k == 0:
                V[i,j,k,i+1,j,k] = 1
                V[i,j,k,i,j+1,k] = 1
                V[i,j,k,i,j,k+1] = 1
                #V(i,j,k,i-1,j,k) = -1
                V[i,j,k,i,j-1,k] = 1
                #V(i,j,k,i,j,k-1) = -1
                V[i,j,k,i,j,k] = -4
                A[i,j,k]=0
            if k == l-1:
                V[i,j,k,i+1,j,k] = 1
                V[i,j,k,i,j+1,k] = 1
                #V(i,j,k,i,j,k+1) = 1
                #V(i,j,k,i-1,j,k) = -1
                V[i,j,k,i,j-1,k] = 1
                V[i,j,k,i,j,k-1] = 1
                V[i,j,k,i,j,k] = -4
                A[i,j,k]=0
        if j == 0 :
            if k != 0 and k != l-1:
                V[i,j,k,i+1,j,k] = 1
                V[i,j,k,i,j+1,k] = 1
                V[i,j,k,i,j,k+1] = 1
                #V(i,j,k,i-1,j,k) = -1
                #V(i,j,k,i,j-1,k) = -1
                V[i,j,k,i,j,k-1] = 1
                V[i,j,k,i,j,k] = -4
                A[i,j,k]=0       
            if k == 0:
                V[i,j,k,i+1,j,k] = 1
                V[i,j,k,i,j+1,k] = 1
                V[i,j,k,i,j,k+1] = 1
                #V(i,j,k,i-1,j,k) = -1
                #V(i,j,k,i,j-1,k) = -1
                #V(i,j,k,i,j,k-1) = -1
                V[i,j,k,i,j,k] = -3
                A[i,j,k]=0
            if k == l-1:
                V[i,j,k,i+1,j,k] = 1
                V[i,j,k,i,j+1,k] = 1
                #V(i,j,k,i,j,k+1) = 1
                #V(i,j,k,i-1,j,k) = -1
                #V(i,j,k,i,j-1,k) = -1
                V[i,j,k,i,j,k-1] = 1
                V[i,j,k,i,j,k] = -3
                A[i,j,k]=0
        if j == l-1:
            if k != 0 and k != l-1:
                V[i,j,k,i+1,j,k] = 1
                #V(i,j,k,i,j+1,k) = 1
                V[i,j,k,i,j,k+1] = 1
                #V(i,j,k,i-1,j,k) = -1
                V[i,j,k,i,j-1,k] = 1
                V[i,j,k,i,j,k-1] = 1
                V[i,j,k,i,j,k] = -4
                A[i,j,k]=0            
            if k == 0:
                V[i,j,k,i+1,j,k] = 1
                #V(i,j,k,i,j+1,k) = 1
                V[i,j,k,i,j,k+1] = 1
                #V(i,j,k,i-1,j,k) = -1
                V[i,j,k,i,j-1,k] = 1
               # V(i,j,k,i,j,k-1) = -1
                V[i,j,k,i,j,k] = -3
                A[i,j,k]=0
            if k == l-1:
                V[i,j,k,i+1,j,k] = 1
                #V(i,j,k,i,j+1,k) = 1
                #V(i,j,k,i,j,k+1) = 1
                #V(i,j,k,i-1,j,k) = -1
                V[i,j,k,i,j-1,k] = 1
                V[i,j,k,i,j,k-1] = 1
                V[i,j,k,i,j,k] = -3
                A[i,j,k]=0              
    if i == l-1:
        if j != 0 and j != l-1:
            if k != 0 and k!= l-1:
                #V(i,j,k,i+1,j,k) = 1
                V[i,j,k,i,j+1,k] = 1
                V[i,j,k,i,j,k+1] = 1
                V[i,j,k,i-1,j,k] = 1
                V[i,j,k,i,j-1,k] = 1
                V[i,j,k,i,j,k-1] = 1
                V[i,j,k,i,j,k] = -5
                A[i,j,k]=0
            if k == 0:
                #V(i,j,k,i+1,j,k) = 1
                V[i,j,k,i,j+1,k] = 1
                V[i,j,k,i,j,k+1] = 1
                V[i,j,k,i-1,j,k] = 1
                V[i,j,k,i,j-1,k] = 1
                #V(i,j,k,i,j,k-1) = -1
                V[i,j,k,i,j,k] = -4
                A[i,j,k]=0
            if k == l-1:
                #V(i,j,k,i+1,j,k) = 1
                V[i,j,k,i,j+1,k] = 1
                #V(i,j,k,i,j,k+1) = 1
                V[i,j,k,i-1,j,k] = 1
                V[i,j,k,i,j-1,k] = 1
                V[i,j,k,i,j,k-1] = 1
                V[i,j,k,i,j,k] = -4
                A[i,j,k]=0
        if j == 0 :
            if k != 0 and k != l-1:
                #V(i,j,k,i+1,j,k) = 1
                V[i,j,k,i,j+1,k] = 1
                V[i,j,k,i,j,k+1] = 1
                V[i,j,k,i-1,j,k] = 1
                #V(i,j,k,i,j-1,k) = -1
                V[i,j,k,i,j,k-1] = 1
                V[i,j,k,i,j,k] = -4
                A[i,j,k]=0       
            if k == 0:
                #V(i,j,k,i+1,j,k) = 1
                V[i,j,k,i,j+1,k] = 1
                V[i,j,k,i,j,k+1] = 1
                V[i,j,k,i-1,j,k] = 1
                #V(i,j,k,i,j-1,k) = -1
                #V(i,j,k,i,j,k-1) = -1
                V[i,j,k,i,j,k] = -3
                A[i,j,k]=0
            if k == l-1:
                #V(i,j,k,i+1,j,k) = 1
                V[i,j,k,i,j+1,k] = 1
                #V(i,j,k,i,j,k+1) = 1
                V[i,j,k,i-1,j,k] = 1
                #V(i,j,k,i,j-1,k) = -1
                V[i,j,k,i,j,k-1] = 1
                V[i,j,k,i,j,k] = -3
                A[i,j,k]=0
        if j == l-1:
            if k != 0 and k != l-1:
                #V(i,j,k,i+1,j,k) = 1
                #V(i,j,k,i,j+1,k) = 1
                V[i,j,k,i,j,k+1] = 1
                V[i,j,k,i-1,j,k] = 1
                V[i,j,k,i,j-1,k] = 1
                V[i,j,k,i,j,k-1] = 1
                V[i,j,k,i,j,k] = -4
                A[i,j,k]=0            
            if k == 0:
                #V(i,j,k,i+1,j,k) = 1
                #V(i,j,k,i,j+1,k) = 1
                V[i,j,k,i,j,k+1] = 1
                V[i,j,k,i-1,j,k] = 1
                V[i,j,k,i,j-1,k] = 1
               # V(i,j,k,i,j,k-1) = -1
                V[i,j,k,i,j,k] = -3
                A[i,j,k]=0
            if k == l-1:
                #V(i,j,k,i+1,j,k) = 1
                #V(i,j,k,i,j+1,k) = 1
                #V(i,j,k,i,j,k+1) = 1
                V[i,j,k,i-1,j,k] = 1
                V[i,j,k,i,j-1,k] = 1
                V[i,j,k,i,j,k-1] = 1
                V[i,j,k,i,j,k] = -3
                A[i,j,k]=0        
    return Nonefor i in range(l):
    for j in range(l):
        for k in range(l):
            FillMatrix(i,j,k)

#Set voltage equation for V+
V[(l-1)/2,(l-1)/2,(l-1)/2,(l-1)/2,(l-1)/2,(l-1)/2] = 7
V[(l-1)/2,(l-1)/2,(l-1)/2,(l-1)/2 -1,(l-1)/2,(l-1)/2] = -1           
V[(l-1)/2,(l-1)/2,(l-1)/2,(l-1)/2,(l-1)/2 -1,(l-1)/2] = -1
V[(l-1)/2,(l-1)/2,(l-1)/2,(l-1)/2,(l-1)/2,(l-1)/2 -1] = -1
V[(l-1)/2,(l-1)/2,(l-1)/2,(l-1)/2 +1,(l-1)/2,(l-1)/2] = -1
V[(l-1)/2,(l-1)/2,(l-1)/2,(l-1)/2,(l-1)/2 +1,(l-1)/2] = -1
V[(l-1)/2,(l-1)/2,(l-1)/2,(l-1)/2,(l-1)/2,(l-1)/2 +1] = -1
V[(l-1)/2,(l-1)/2,(l-1)/2,(l+1)/2,(l+1)/2,(l+1)/2] = 1   V[(l+1)/2,(l+1)/2,(l+1)/2,(l-1)/2,(l-1)/2,(l-1)/2] = -1        
V[(l+1)/2,(l+1)/2,(l+1)/2,(l+1)/2,(l+1)/2,(l+1)/2] = -7         current = 50  #change this to anything you want and you should get 0.0261768888518 ohms for l = 17
A[(l-1)/2,(l-1)/2,(l-1)/2] = (current)                       
A[(l+1)/2,(l+1)/2,(l+1)/2] = (-1)*current                         
                                
x = linalg.tensorsolve(V,A)  
R_equivalent = (x[(l-1)/2,(l-1)/2,(l-1)/2]-x[(l+1)/2,(l+1)/2,(l+1)/2])/current
print("R_equivalent: ")
print R_equivalent

So I just realized this, but I had set l=3, meaning a 3x3x3 cube. For this value I get .219, which is consistent with the averaging method. However, when I change it to anything higher, I get something of the order of -16... which is not consistent with the averaging method. Every single point is spiking to 25 volts (I used a fixed current flowing out of V+ and into V- and allowed the voltages to vary dynamically). My guess would be that I have a mistake in my coefficients, and that "current is being stored" in the nodes.

Any ideas for this last one? I can answer questions about the code if you have any.

 

[mfb]

avg = total/6

Not always 6, unless you fix the voltage at the border to 0 (but then you could save all the casework). Setting the border to a fixed 2.5 V should work, if you use the array borders then you don't need all the subcases for the averaging process. Just skip the borders in the update.

You are overwriting nodes while you are still processing neighbor nodes. That can lead to unexpected effects. A copy of the array should work better.

No change in the result, but probably easier: instead of the if/elseif condition in the innermost loop, you can overwrite the nodes (if you work with a copy: see above) and end an iteration by setting the values again.

 

[BiGyElLoWhAt]

I did fix the borders to zero, or beyond the borders, I should say. I'm treating them as infinitely far away, so the voltage between that and ground is zero.

I didn't think about the fact that I was overwriting values. Thanks for that.

 

[mfb]

You should set them to the average of the two "input" nodes - that is the approximate voltage a truly infinite grid would have far away due to symmetry. There is nothing special about zero.