Separ8shun said:
(apart from 'pushed back'. i assume you mean that the pressure increases with distance along the chord resulting in a net force acting upstream? if you don't mean that then i am in BIIIIIIGG trouble!)
Yes. This image on Wikipedia illustrates what an adverse pressure gradient does to a boundary layer the farther downstream you go.
Separ8shun said:
The examples you mentioned are good. I knew about them before but if you could describe (or link to) how they create that favourable pressure gradient or re-energise the flow that would be outstanding.
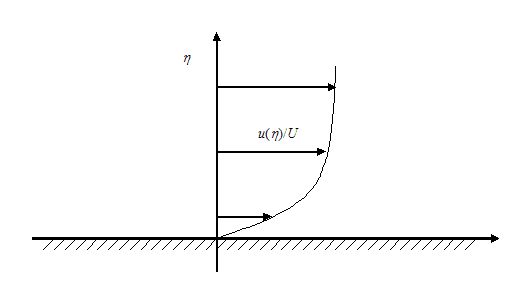
Since you have an aerospace engineering degree, I presume you know a bit about airfoils. As air moves over the top, it accelerates. This is indicative of a favorable pressure gradient. However, once it reaches the pressure minimum and the airfoil begins tapering back towards the trailing edge, the flow slows down indicating an adverse pressure gradient. When there is a favorable pressure gradient, there is nothing to cause that little "hitch" in the boundary layer profile and it looks like a typical (or slightly fuller) Blasius boundary layer (below). Injecting momentum in the form of wall parallel jets counteracts the effects of an adverse pressure gradient by helping push that little hitch back out. Suction works similarly by helping pull the high-momentum fluid down and filling out the profile that way.
Separ8shun said:
Could you elaborate on how rough surfaces create transition. It seems fairly obvious but i have not seen any scientific wording and all i have is 'rough surfaces disrupt the smooth layers of laminar flow by inconsistent shear stress due to random surface geometry' which sounds like crap but is all i can come up with off the top of my head. It is something to replace that statement that i am hoping to find.
The other method i am interested in is the designing the aerofoil to have a favourable pressure gradient (I think this is called a supercritical flow and involves moving the point of max thickness aft as far as possible and flattening the upper surface of the wing though i am not certain). Could you explain/link to how this works in terms of pressures, shear stresses and velocities?
I'm not sure if this is too deep into the subject to be easily explained, but if it is then please just say.
Every boundary layer is essentially just a complicated dynamical system. As such, the Navier-Stokes equations can by broken down through a stability analysis into the
Orr-Sommerfeld equation. This essentially constitutes an eigenvalue problem, meaning a number of different modes can satisfy the equation and grow at a variety of different rates. Like any other dynamical system, it is sensitive to perturbations of certain frequencies and types and not very sensitive to perturbations of certain other frequencies and types.
It is also important to note that boundary layers with inflection points in them (i.e. \frac{\partial^2 u}{\partial y^2} = 0 somewhere in the profile) are incredibly unstable. This is called the Rayleigh criterion. I won't go into its derivation unless you want to see it, but it probably would warrant its own post.
There are a variety of different instabilitiy mechanisms, but there are three that dominate nearly every type of subsonic wing (with slight additional complications when moving into the supersonic regime). The first are
Tollmien-Schlichting waves. These dominate the transition process of most two-dimensional boundary-layers such as over a flat plate or on a 2-D wing. They are essentially sound waves that get trapped in the boundary layer.
Next, on any surface with concave curvature (such as wind tunnel nozzles or near the trailing edge of some airfoils, you see the
Görtler vortices develop. These are counter-rotating vortices that align themselves with the streamlines and convect downstream, modifying the mean-flow such that secondary, inflectional instabilities develop and lead to transition. This can also happen on a convex surface that is rotating through a fluid.
The third type of instability is what is called attachment line contamination. A boundary layer develops over the fuselage of planes, and this is pretty much always turbulent no matter what. On a swept wing, this turbulent boundary layer can continue on down the attachment line of the swept wing and cause the entire boundary layer over the wing to be turbulent as a result. This is fairly easy to fix using a Gaster bump, which essentially just involves creating a point on the wing near the root that serves as a stagnation point and causes the turbulent fuselage boundary layer to continue down the wing near the root and allows a fresh, laminar boundary layer to form at that stagnation point and travel down the wing.
The final major instability is the crossflow instability, which develops on swept wings. On a swept wing, the pressure gradient over the wing combined with sweep leads to a phenomenon where the inviscid streamlines do not line up perfectly with the streamlines at the wall. This means the boundary layer is three-dimensional and has an inflection point in it, which is unstable. The result is streamwise (w.r.t. the inviscid streamlines), co-rotating vortices that eventually cause breakdown much like Görtler vortices, through mean flow distortion and secondary instability breakdown.
These are all primary instability modes. The overall transition process can be described graphically with the following "roadmap" originally created by Morkovin:
http://upload.wikimedia.org/wikipedia/en/d/dc/Pathtotransition.PNG
Surface roughness comes into play in the "receptivity" phase of the process. You start out with disturbance in the free stream. These come in the form of acoustic disturbances (sound waves), vortical disturbances (turbulence) and entropy disturbances (temperature fluctuations). Different instability modes are sensitive to different types of disturbances, in particular the acoustic and vortical disturbances. For a given free stream, the disturbances maybe be of any variety of sizes and magnitudes. When it comes to flight or a well-designed wind tunnel, these disturbances are very small and generally on a fairly large scale.
Going back to what I said earlier, boundary layers are only sensitive to perturbations of specific scales and frequencies as determined by linear stability theory. Other disturbances die out (except in the case of transient growth, which is a whole other animal). Environmental disturbances are rarely of a scale that readily excites a boundary layer, so something has to provide a means for their scales to be changed to those to which the boundary layer is receptive. Surface roughness is this mechanism. Free-stream disturbances interact with surface roughness. They are diffracted and enter into the boundary layer as the tiny initial conditions in the stability problem. From there they grow according to the characteristics of the boundary layer.
In general, T-S waves are sensitive to acoustic disturbances and 2-D steps and can be stabilized with a favorable pressure gradient (the basis for the concept of Natural Laminar Flow [NLF] airfoils, which are similar to what you described here). Crossflow is sensitive to 3-D roughness and vortical disturbances and is destabilized by a favorable pressure gradient (making it arguably the most difficult to control). The methods for controlling these primary modes are collectively known as Laminar Flow Contro (LFC)l, and to get a good read on all of the strategies that have been employed, I would have to again point you to that Joslin paper, which is reasonably light on the technical side and is instead more like 29 pages of fairly general overview (with figures!).
Surface suction has shown to be effective at controlling all of these mechanisms, but hasn't been implemented commercially because the added maintenance cost of the suction system is too high to be worth the fuel savings. The focus lately has been on designing using many of the NLF concepts to prevent growth of T-S waves and attachment line contamination, which is very unstable to crossflow, so all further attention can be directed there. There are a couple potential options being researched for controlling crossflow specifically, but again, for the sake of brevity, I won't go into that in this post.
Supercritical airfoils are a different topic and involve transonic flight and controlling the Mach number that is achieved over the wing to minimize the effects of shocks or prevent said effects entirely. This is similar to but not identical to NLF. I am not 100% familiar with designing a supercritical airfoil, so if that is really your goal, then I can't really elaborate. NLF is much as you have described but also involves considerations on the radius of the leading edge to help control the attachment line boundary layer. Also of note is that the combination of NLF with surface suction is a technique known as Hybrid LFC.
Hopefully that was helpful. It may be a bit disjoint, as I wrote this largely during breaks from writing a different paper, so I may sound a bit crazy, haha.