Derivation of the change of air pressure with height

[Adesh]

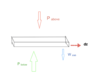
If we take a slab of air with cross-sectional area of A and height dz in our atmosphere. Now, what we do is make an argument like this :-

Pressure from below must balance both the weight and Pressure from above to keep the slab at rest. ( I have added an attachment for clarification)

And from this are argument we do something like this :
P_{above} = P
W_{slab} = mg , Pressure from weight is \rho \times A \times dz \times / A = \rho ~dz~g ( \rho is the density of air)

Therefore, P_{below} = P + \rho~dz~g

dP = P_{above} - P_{below} = - \rho ~dz~g

\frac{dP} {dz} = - \rho ~g

Now, my question is why we didn't not take into account the weight of air which is above the slab? I mean the air which lies above our sample slab must have weight this weight would have been pushing our slab downwards and therefore pressure from below must also balance this. The mass of air which lies above the slab must have number molecules and gravity would attract them and we should center of mass and assume the gravity to act over there and this force of gravity should cause a pressure on our slab.

I tried to argue that pressure from above is due to weight of air only, but after sometime I thought that this argument is not good as fluid causes pressure due to collision of it's molecules .

So, I want to restate my problem again : Why in our derivation we didn't take into account the pressure caused by the weight of the air that lies above our slab?

Thank you, any help will be much appreciated. I tried to be as clear as I could be.

 

[DrStupid]

So, I want to restate my problem again : Why in our derivation we didn't take into account the pressure caused by the weight of the air that lies above our slab?

What do you think what $P_{above}$ is?

 

[Adesh]

What do you think what $P_{above}$ is?

It is the collision of air molecules.

 

[DrStupid]

It is the collision of air molecules.

That's the microscopic view. From a macroscopic point of view pressure is force per area. In case of $P_{above}$ this force comes from the air above. Do you agree?

 

[Dale]

Now, my question is why we didn't not take into account the weight of air which is above the slab?

The weight of the air above does not act on the slab of air. Why would we include it in the forces on the slab?

When you do a free body diagram you include only forces acting on the body in question. In this case there are three such forces on the slab: the pressure from above the slab, the pressure from below the slab, and the weight of the slab. The weight of the air above does not act on the slab. Including it would be wrong.

 

[Adesh]

That's the microscopic view. From a macroscopic point of view pressure is force per area. In case of $P_{above}$ this force comes from the air above. Do you agree?

Yes.

 

[Adesh]

The weight of the air above does not act on the slab of air. Why would we include it in the forces on the slab?

When you do a free body diagram you include only forces acting on the body in question. In this case there are three such forces on the slab: the pressure from above the slab, the pressure from below the slab, and the weight of the slab. The weight of the air above does not act on the slab. Including it would be wrong.

That's what I want to know. Why including it will be wrong?

 

[Dale]

Why including it will be wrong?

Because it doesn’t act on the slab. Only forces acting on the slab should be included.

 

[Adesh]

Because it doesn’t act on the slab. Only forces acting on the slab should be included.

So on what it acts?

 

[Dale]

So on what it acts?

The weight of the air above acts on the air above. Is that somehow not obvious?

The weight of any object is the gravitational force acting on that object. The thing that it acts on is literally part of the definition of the weight. How can this be unclear?

What do you think weight is?

 

[DrStupid]

Yes.

OK, the air exerts a downward force. According to the 3rd law there must be a corresponding counterforce, acting upward on the Earth and according to the 2nd law the air would be accelerated if this would be the only force acting on it. But in the static case the air doesn't accelerate. Therefore there must be another force acting on the air. Do you agree? If yes, which force is it?

 

[Chestermiller]

The weight of the air above is captured in the pressure above, $p_{above}$

 

[Adesh]

The weight of the air above is captured in the pressure above, $p_{above}$

Really? thank you I had same thought but I was fearing that I would be wrong.

 

[Adesh]

The weight of the air above acts on the air above. Is that somehow not obvious?

The weight of any object is the gravitational force acting on that object. The thing that it acts on is literally part of the definition of the weight. How can this be unclear?

What do you think weight is?

If I hold a heavy sack on my head won't I feel that something is pushing me down? That feeling of pushing down is because I'm barring the sack from falling due gravity and hence applying a force equal and against the gravity.

 

[Adesh]

OK, the air exerts a downward force. According to the 3rd law there must be a corresponding counterforce, acting upward on the Earth and according to the 2nd law the air would be accelerated if this would be the only force acting on it. But in the static case the air doesn't accelerate. Therefore there must be another force acting on the air. Do you agree? If yes, which force is it?

Sir, what I'm saying is: the air which lies above the slab would have it's weight just like our slab has a weight and weight always acts downwards, therefore slab must be bearing the weight of the air above it (just like we bear the weight of something if we hold it over our head).

 

[DrStupid]

Sir, what I'm saying is: the air which lies above the slab would have it's weight just like our slab has a weight and weight always acts downwards

I just assume that to be the answer to my last question.

therefore slab must be bearing the weight of the air above it (just like we bear the weight of something if we hold it over our head).

"bearing the weight" means exerting an upward force that compensates the weight. In this case it is the upward force I was talking about in #11. Does that tell you something about the origin of $P_{above}$?

 

[Herman Trivilino]

If I hold a heavy sack on my head won't I feel that something is pushing me down?

Sure. It's the sack pushing on your head. It's a contact force, often called the normal force in elementary physics problems. It's not the weight of the sack (which is a force exerted on the sack by Earth).

That feeling of pushing down is because I'm barring the sack from falling due gravity and hence applying a force equal and against the gravity.

You're applying a force on the sack that's equal and opposite to the force the sack exerts on you (Newton's Third Law). The reason the sack doesn't fall is because the force you exert on it is equal to the force Earth exerts on it (Newton's Second Law).

 

[Dale]

If I hold a heavy sack on my head won't I feel that something is pushing me down? That feeling of pushing down is because I'm barring the sack from falling due gravity and hence applying a force equal and against the gravity.

You are misunderstanding the physics. The feeling of something pushing you down is entirely due to the contact force (pressure) on your head. If you reduce the contact force without changing the weight then the feeling reduces. If you reduce the weight without changing the contact force then the feeling is unchanged.

The feeling is not due to the weight, it is due to the pressure. The weight of the sack acts on the sack, not on me. Only the contact force from the sack acts on me, not it’s weight.

 

[Adesh]

I just assume that to be the answer to my last question.
Means P_{above} is just the weight of the air lying above it, okay. I was thinking that it is the pressure caused due to collision of molecules of air with our sample slab. Thank you. You have explained it in a nice way"bearing the weight" means exerting an upward force that compensates the weight. In this case it is the upward force I was talking about in #11. Does that tell you something about the origin of $P_{above}$?

 

[Adesh]

You are misunderstanding the physics. The feeling of something pushing you down is entirely due to the contact force (pressure) on your head. If you reduce the contact force without changing the weight then the feeling reduces. If you reduce the weight without changing the contact force then the feeling is unchanged.

The feeling is not due to the weight, it is due to the pressure. The weight of the sack acts on the sack, not on me. Only the contact force from the sack acts on me, not it’s weight.

Sir, I think due to my mistake of using the word “weight” as the acting force on something is causing the confusion.
I meant by “weight” the force mg which I must provide to something to keep it from falling. So if I’ holding a sack on my head, I need to apply a force equal to its weight and this force is being applied by itself due Newton’s 3rd Law but I have to stay up for 3rd Law to work. Since both forces are acting ( my force and sack’s weight) on different objects therefore I would feel something heavy or being pushed down feeling.
Let me know if my essence of understanding is wrong over here. I have got a great chance to amend it ( if it’s wrong) from great mentors like you. Thank you.

 

[Dale]

I meant by “weight” the force mg which I must provide to something to keep it from falling.

First, that force is the contact force, not the weight. Second, in many situations the contact force will not be equal to mg.

therefore I would feel something heavy or being pushed down feeling.

Yes, that is the contact force, or in other words the pressure. Any influence that the weight of the upper object might have is transmitted to the lower object through the pressure. Once you have accounted for the contact force (pressure) then you have already accounted for the weight of the upper object.

 

[Adesh]

First, that force is the contact force, not the weight. Second, in many situations the contact force will not be equal to mg.

Yes, that is the contact force, or in other words the pressure. Any influence that the weight of the upper object might have is transmitted to the lower object through the pressure. Once you have accounted for the contact force (pressure) then you have already accounted for the weight of the upper object.

What about the pressure caused due to collision of molecules?

 

[Dale]

What about the pressure caused due to collision of molecules?

Can you be more specific with your question?

 

[Adesh]

Can you be more specific with your question?

There may be two kinds of pressure:-

1. Defined by you as the contact force.

2. Pressure due to collision of molecules with the walls of container that we use in thermodynamics . So the air above the slab must be colliding with our slab and hence may be causing some collisional pressure.

 

[vanhees71]

I think, you already had the right ansatz in #1. Just use the general equation
$$\vec{\nabla} p=-\rho g.$$
We need an equation of state. A good ansatz is the polytrope
$$p=p_0 (\rho/\rho_0)^n,$$
where $p_0$ and $\rho_0$ are the pressure at height $z=0$. Since the pressure and density change only along $z$, we have
$$\mathrm{d}_z p=-g \rho_0 (p/p_0)^{1/n}$$
with the solution
$$p(z)=p_0 \left (1-\frac{n-1}{n} \frac{\rho_0}{p_0} g z \right)^{n/(n-1)}.$$
For $n=1$ (isothermal equation of state for an ideal gas) we have
$$\mathrm{d}_z p=-g p \rho_0/p_0$$
and thus
$$p(z)=p_0 \exp \left (-\frac{g \rho_0}{p_0} z \right).$$
On the other hand
$$p_0=\rho_0 k T/m,$$
where $k$ is Boltzmann's constant, $T$ the (absolute) temperature, and $m$ the mass of the gas molecules,
$$p(z)=p_0 \exp \left (-\frac{g m}{k T} z \right).$$
This is the barometric formula for an isothermal atmosphere.

 

[Dale]

There may be two kinds of pressure:-

1. Defined by you as the contact force.

2. Pressure due to collision of molecules with the walls of container that we use in thermodynamics . So the air above the slab must be colliding with our slab and hence may be causing some collisional pressure.

Sure. 1 is the pressure for a solid (your sack/head example), 2 is the pressure for a gas (the OP situation).

What is the question?

 

[Adesh]

Sure. 1 is the pressure for a solid (your sack/head example), 2 is the pressure for a gas (the OP situation).

What is the question?

Does the weight of air same as the pressure exerted by it? (That collisional pressure)

 

[Chestermiller]

Does the weight of air same as the pressure exerted by it? (That collisional pressure)

What exactly is collisional pressure and how does it differ from just plain old pressure?

 

[Dale]

Does the weight of air same as the pressure exerted by it?

No, it is not the same. The weight is a gravitational force. The pressure is a “collisional” force as you put it. Even in situations where the magnitude of the forces are the same they are still distinct forces originating from different physical interactions

 

[Adesh]

What exactly is collisional pressure and how does it differ from just plain old pressure?

Plain old pressure? Sir I haven’t understood your allusion.

Collisional pressure is the pressure caused by fluids, such as on piston or walls of container containing it. So, if we take a slab of air then molecules from above would cause collisional pressure on the slab and the weight of the air above would cause additional pressure. This is the problem, why we didn’t take that pressure from weight into our account.

 

[Dale]

if we take a slab of air then molecules from above would cause collisional pressure on the slab and the weight of the air above would cause additional pressure

This is incorrect. All of the pressure is “collisional”, including whatever pressure might be related to the weight of the gas. There is no additional pressure.

 

[Adesh]

This is incorrect. All of the pressure is “collisional”, including whatever pressure might be related to the weight of the gas. There is no additional pressure.

But here you have said that it’s not same

No, it is not the same. The weight is a gravitational force. The pressure is a “collisional” force as you put it. Even in situations where the magnitude of the forces are the same they are still distinct forces originating from different physical interactions

 

[Dale]

Yes. The pressure is not the weight. All of the pressure is collisional, all of the weight is gravitational. What is at all unclear here?

I cannot believe that this is confusing. Draw a free body diagram for the slab of air.

 

[Adesh]

Yes. The pressure is not the weight. All of the pressure is collisional, all of the weight is gravitational. What is at all unclear here?

I cannot believe that this is confusing. Draw a free body diagram for the slab of air.

Wouldn’t gravity going to attract the air above the slab and since the slab lies below therefore it has to bear that force by which gravity is pulling the air above. So slab must have be having some pressure from below which should balance both collisional pressure and force of gravity of air above.

 

[Dale]

Please draw the free body diagram, as requested. Also, label each force and identify:
1) the type of force
2) the object providing the force (I.e. the other object in the third law pair for each force)

 

[Chestermiller]

Plain old pressure? Sir I haven’t understood your allusion.

Collisional pressure is the pressure caused by fluids, such as on piston or walls of container containing it. So, if we take a slab of air then molecules from above would cause collisional pressure on the slab and the weight of the air above would cause additional pressure. This is the problem, why we didn’t take that pressure from weight into our account.

If you do a force balance in the fluid above, the pressure from below times the area is equal to the weight of the fluid above.

 

[Adesh]

Please draw the free body diagram, as requested. Also, label each force and identify:
1) the type of force
2) the object providing the force

That Weight_{air} is weight of the air which lies above the slab .

 

[Dale]

$Weight_{air}$ does not act on the slab. It does not belong on the free body diagram for the slab.

 

[Adesh]

If you do a force balance in the fluid above, the pressure from below times the area is equal to the weight of the fluid above.

Yes sir.

 

[Adesh]

$Weight_{air}$ does not act on the slab. It does not belong on the free body diagram for the slab.

It acts on air above but slab is bearing that.

 

[Dale]

It acts on air above but slab is bearing that.

So what? That is completely irrelevant for the free body diagram of the slab. Only forces acting on the body itself are included in a free body diagram. Were you not taught this?

 

[Adesh]

So what? That is completely irrelevant for the free body diagram of the slab.

Why? Weight of air is pushing the slab downwards, collisional pressur eis pushing the slab downwards and the grravity too is attracting it downwards. Why my words are not making sense to you?

 

[Dale]

Why?

Because in a free body diagram you only include forces directly acting on the free body.

Why my words are not making sense to you?

This is not a communication problem. You have a conceptual physics misunderstanding and instead of correcting it you are trying to explain why you are right. You are wrong. You are analyzing the situation incorrectly. The mistake you are making is demonstrated by the incorrect inclusion of the $Weight_{air}$ force in the free body diagram of the slab. It doesn’t belong there and including it is wrong.

 

[Chestermiller]

Yes sir.

OK. So, if z is the elevation at the top of the slab, this means that $$p(z)=\int_z^{\infty}{\rho(\xi) g d\xi}$$where $\xi$ is a dummy variable of integration (representing elevations above z). This says that the weight per unit horizontal area of the fluid above z (right hand side) is equal to the pressure at z. Do you agree with this equation?

 

[DrStupid]

There may be two kinds of pressure:-

1. Defined by you as the contact force.

2. Pressure due to collision of molecules with the walls of container that we use in thermodynamics . So the air above the slab must be colliding with our slab and hence may be causing some collisional pressure.

They are identical.

 

[Dale]

@Adesh let me explain how to analyze forces and draw a free body diagram.

Each force represents an interaction between two bodies. A contact force is a surface interaction between two bodies that are touching. Tension is a similar interaction between a rope or cable and another body. Pressure is a “collisional” interaction between a fluid and another body. Weight is a gravitational interaction between the Earth and a body, etc.

For each interaction we have in a scenario we can describe the type of interaction and the two bodies that are interacting.

In this case we have four bodies: the earth, the slab, the air above, and the air below. There is a gravitational interaction between the Earth and the air above. There is a gravitational interaction between the Earth and the slab. There is a gravitational interaction between the Earth and the air below. There is pressure between the air above and the slab. There is pressure between the slab and the air below. There is pressure between the air below and the earth.

This is a complete list of the important interactions in this scenario. Note that there is no pressure interaction between bodies that are not touching, and there is no gravitational interaction between the various air bodies.

Each interaction involves two forces, one acting on each of the two different bodies, and Newton’s third law says that these forces are equal and opposite. When you draw a free body diagram you include all of the forces that act on that body and none of the forces acting on other bodies.

Note, in the list of interactions I highlighted each occurrence of the slab. The slab occurred in three interactions, so there should be exactly three forces on its free body diagram. One is the pressure from the top, one is the pressure from the bottom, and the other is the weight of the slab.

The weight of the top air is not included because it does not act on the slab. It is an interaction between the top air and the earth, so it would be included in a free body diagram for the top air or for the earth. It is wrong to include it on a free body diagram of the slab.

I hope this systematic approach helps you understand how to analyze a scenario and correctly draw the free body diagrams. Once you have correctly drawn a free body diagram then you can apply Newton’s second law to analyze the dynamics of that body.

 

[Adesh]

OK. So, if z is the elevation at the top of the slab, this means that $$p(z)=\int_z^{\infty}{\rho(\xi) g d\xi}$$where $\xi$ is a dummy variable of integration (representing elevations above z). This says that the weight per unit horizontal area of the fluid above z (right hand side) is equal to the pressure at z. Do you agree with this equation?

Wow. What a great explanation! I’ll always be grateful to you.

 

[vanhees71]

It's not as simple since to close the hydrodynamic equations you need an equation of state, i.e., a relation between pressure and density. See my posting #25 for the full calculation, using they polytropic ansatz (valid, e.g., for ideal gases for an adiabatic or isothermal atmosphere).

 

[Herman Trivilino]

What about the pressure caused due to collision of molecules?

The force caused by the collision of molecules is the contact force I referred to in Post #17. That is the force you feel. You can't possibly feel the weight $mg$ of the sack. You can prove this to yourself by setting the sack down on the floor. The weight $mg$ of the sack doesn't go away when you do that, but the force exerted on your head by the sack does go away.

Forces are interactions between objects. They are not properties of objects.

 

[Chestermiller]

Wow. What a great explanation! I’ll always be grateful to you.

You should really be thanking @Dale and the others. This equation that I wrote is fully consistent with what they have been saying. You can see that now, right?