hastings
- 80
- 0
Hi everyone!
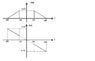
I was trying to solve an old exercise but in a different way. It asks to find the signal x(t) given the graphs of |X(f)| and arg[X(f)]. Please refer to the attachment.
My stategy this time is as follows:
1) find D(f) by deriving |X(f)|
2) antitransform D(f) and get d(t)
3) divide by -j2πt and finally get x(t)
So the first step is finding D(f). From a similarly worked out problem I gathered it should be
D(f)= \frac{1}{16} \text{rect}_{4W}(f+4W) - \frac{1}{16} \text{rect}_{4W}(f-4W)
However I'm not sure whether the following addend should also be included in D(f):
-\frac{1}{4}W \delta(f+2W)+\frac{1}{4}W \delta(f-2W)
So ultimately it should be
D(f)= \frac{1}{16} \text{rect}_{4W}(f+4W) - \frac{1}{16} \text{rect}_{4W}(f-4W) -\frac{1}{4}W \delta(f+2W)+\frac{1}{4}W \delta(f-2W)
Is it right? Or there should be no dirac?
Thank you for your time.
I was trying to solve an old exercise but in a different way. It asks to find the signal x(t) given the graphs of |X(f)| and arg[X(f)]. Please refer to the attachment.
My stategy this time is as follows:
1) find D(f) by deriving |X(f)|
2) antitransform D(f) and get d(t)
3) divide by -j2πt and finally get x(t)
So the first step is finding D(f). From a similarly worked out problem I gathered it should be
D(f)= \frac{1}{16} \text{rect}_{4W}(f+4W) - \frac{1}{16} \text{rect}_{4W}(f-4W)
However I'm not sure whether the following addend should also be included in D(f):
-\frac{1}{4}W \delta(f+2W)+\frac{1}{4}W \delta(f-2W)
So ultimately it should be
D(f)= \frac{1}{16} \text{rect}_{4W}(f+4W) - \frac{1}{16} \text{rect}_{4W}(f-4W) -\frac{1}{4}W \delta(f+2W)+\frac{1}{4}W \delta(f-2W)
Is it right? Or there should be no dirac?
Thank you for your time.