If you do not know how vectors work, it is ok, just imagine that there are no arrows.
tomtomtom1 said:
1) Force can be defined as Mass * Acceleration
Yes, within the folds of Newtonian physics (or Classical mechanics, if you like). If you will take advanced physics courses, you will see that ##\vec F=\dfrac{d\vec p}{dt}## won't necessarily reduce to ##m\vec a##.
tomtomtom1 said:
which is the same thing as saying Force is equal to change of momentum with respect to time, which is the same thing as saying the Force acting on a body is equal to the rate of change of momentum with respect to time
If by "change of momentum with respect to time" you are referring to ##\dfrac{\Delta \vec p}{\Delta t}## and by "rate of change of momentum with respect to time" you mean ##\dfrac{d\vec p}{dt}## then not necessarily!
The first is used when the
acceleration is constant:
$$\begin{align*}
\dfrac{\Delta \vec p}{\Delta t}&=\dfrac{m\vec v(t+\Delta t)-m\vec v(t)}{\Delta t}\text{ where }\vec v(t)=\vec at+\vec v_0\text{ and }\vec v_0\text{ is the initial velocity vector}\\
&=\dfrac{m\vec a*(t+\Delta t)+m\vec v_0-m\vec a*(t)-m\vec v_0}{\Delta t}\\
&=\dfrac{m\vec a*\Delta t}{\Delta t}\\
&= m\vec a
\end{align*}$$
In the second case, i.e the acceleration vector is not constant, the quantity ##\dfrac{\Delta \vec p}{\Delta t}## represents an "
average" net force. To get the "instantaneous" net force, however, you will need to take the time
derivative of momentum, ##\dfrac{d\vec p}{dt}=\lim_{\Delta t\to0}\dfrac{\vec p(t+\Delta t)-\vec p(t)}{\Delta t}## (ignore this if you do not know what it means, for now).
On another note, when the acceleration is constant ##\dfrac{d\vec p}{dt}=\dfrac{\Delta \vec p}{\Delta t}##
tomtomtom1 said:
2) Would it be correct to say that Force is equal to the Change in Momentum DIVIDED by Change in Time i.e Delta p / Delta t (p = momentum, t = time) - would this be a correct statement.
I guess you can answer that yourself from what you should have just read as a response to what has been mentioned :)
tomtomtom1 said:
3) Finally, given the example:-
Car traveling at 40 m/s with a mass of 256kg
After 92 seconds the car is traveling at 45 m/s with a mass of 256kg
Initial Momentum = 40 *256 = 10240
Final Momentum = 45 * 256 = 11520
Change in time = 92 seconds
Change in momentum = 11520 - 10240 = 1280
The force the car is traveling at is = 1280 / 92 = 13.9 Newtons
Dr.
@PhanthomJay answered this for you ;) Note, however, that the force should be considered as an average if the acceleration in your example is not constant.
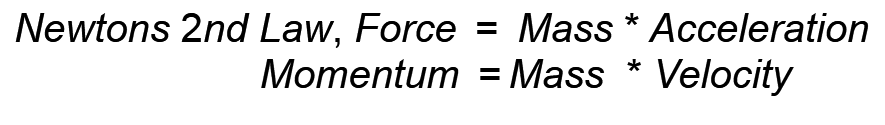
 But i still am struggling to derive the equation of Momentum (Mass * Velocity) from the above equations?
But i still am struggling to derive the equation of Momentum (Mass * Velocity) from the above equations?