mmh37
- 56
- 0
Problem:
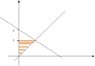
"Draw a Diagram to show over which area the following integral (see integral in attached file) is integrated."
I drew a little diagram of what I think the area looks like (see diagram). But I am very, very insecure about what I did and would appreciate if anyone could have a look at it and let me know if I did something wrong. That would be really helpful!
"Draw a Diagram to show over which area the following integral (see integral in attached file) is integrated."
I drew a little diagram of what I think the area looks like (see diagram). But I am very, very insecure about what I did and would appreciate if anyone could have a look at it and let me know if I did something wrong. That would be really helpful!