allora_97
- 13
- 0
Homework Statement
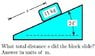
A 11 kg block slides down a frictionless slope
which is at angle θ = 24◦. Starting from rest,
the time to slide down is t = 1.85 s.
The acceleration of gravity is 9.8 m/s2 .
(look at image)
What total distance s did the block slide?
Answer in units of m.
Homework Equations
F=ma
F=mg
tan(theta) = Fy/Fx
The Attempt at a Solution
I calculated the acceleration, a = F/m = 22.01116038m/s^2.
I used the time 1.85sec and the acceleration to find the velocity, v = 40.72064671m/s.
I don't know how to proceed from this point?