- #1
MSG100
- 43
- 0
My problem:
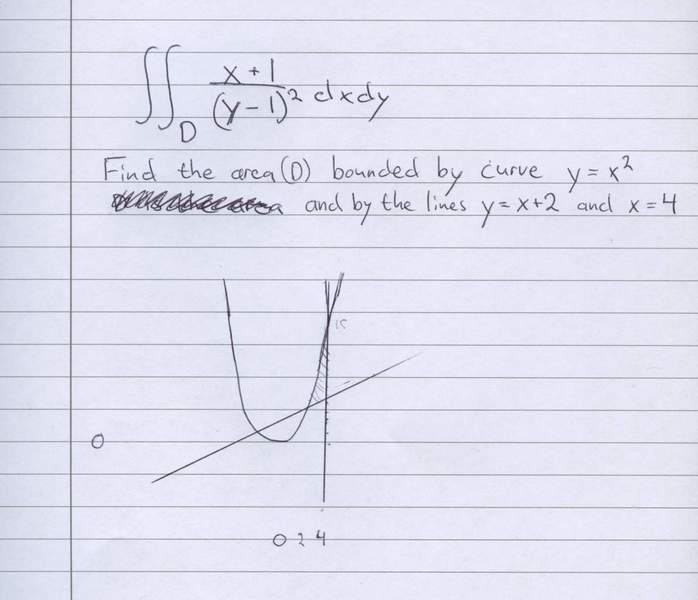
I don't know how to begin with this problem.
I don't know how to begin with this problem.
MSG100 said:
Here's a link to some tips, especially #2 on the list. LaTeX isn't very hard to learn, and you can always use the tags that are available when you click Go Advanced just below the text input area.MSG100 said:I understand. It's messy and hard to follow my calculations. Hopefully I will learn to write in latex soon.
You're very welcome. That's our hope as well, that newcomers will eventually become members who can help the ones coming later.MSG100 said:I don't have the answer but it seems too small, just 0.9 a.u.?
Thanks a lot for the effort you put into helping people like me. Maybe someday we'll be the ones that help others!
A double integral is a mathematical concept used in multivariable calculus to find the volume under a surface in a three-dimensional space. It involves integrating a function over a two-dimensional region.
A regular integral involves finding the area under a curve in a one-dimensional space. In contrast, a double integral involves finding the volume under a surface in a two-dimensional space. It requires integrating over two variables instead of one.
In a double integral, the two lines refer to the limits of integration for the two variables. These lines define the boundaries of the two-dimensional region over which the function is being integrated. The curve represents the function being integrated over this region.
To solve a double integral with two lines and one curve, you first need to determine the limits of integration for the two variables by finding the points of intersection between the lines and the curve. Then, you multiply the function being integrated by the differential of the two variables and integrate over the region defined by the two lines and the curve.
Double integrals have many real-world applications, such as in physics to calculate the mass of an object with varying density, in economics to find the total cost of producing a product with changing prices, and in statistics to determine the probability of an event occurring within a two-dimensional region.