jessedevin
- 66
- 0
Homework Statement
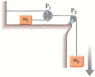
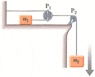
An object of mass m1 on a frictionless horizontal table is connected to an object of mass m2 through a very light pulley P1 and a light fixed pulley P2.
(a) If a1 and a2 are the accelerations of m1 and m2, respectively, what is the relation between these accelerations?
(b) Express the tensions in the strings in terms of g and the masses m1 and m2.
(c) Express the accelerations a1 and a2 in terms of g and the masses m1 and m2.
Homework Equations
\SigmaF = ma
The Attempt at a Solution
The way that I did it was I made two force diagrams. The first force diagram of m1 I made just has force going to the right, force T1 (tension of rope). Then I have a second force diagram of m2 with a force T2 going up and a force of mg (or weight of m2) going down. but the thing is that I keep on getting one a (acceleration), but the answer has a1 and a2. Can someone please tell me what I am doing wrong with my force diagrams. I think if i can have the correct force diagram, then I will be able to do the problem (hopefully!).