Drag on a Supersonic Baseball (from SmarterEveryDay)

[mabraden]

TL;DR Summary

Looking for help explaining surprisingly high drag on a supersonic baseball.

In a recent video from SmarterEveryDay, a baseball is launched from an air cannon faster than the speed of sound. I used the video with my 2nd year HS physics class, and we put the high speed segment of the moving ball into Tracker (video analysis and modeling tool).

We found that the drag coefficient would have to have been around 3, using the speed squared model of drag for high Reynolds numbers. Although we did learn from a little research that drag coefficients aren't constant, I couldn't find any reference to coefficients nearly this high.

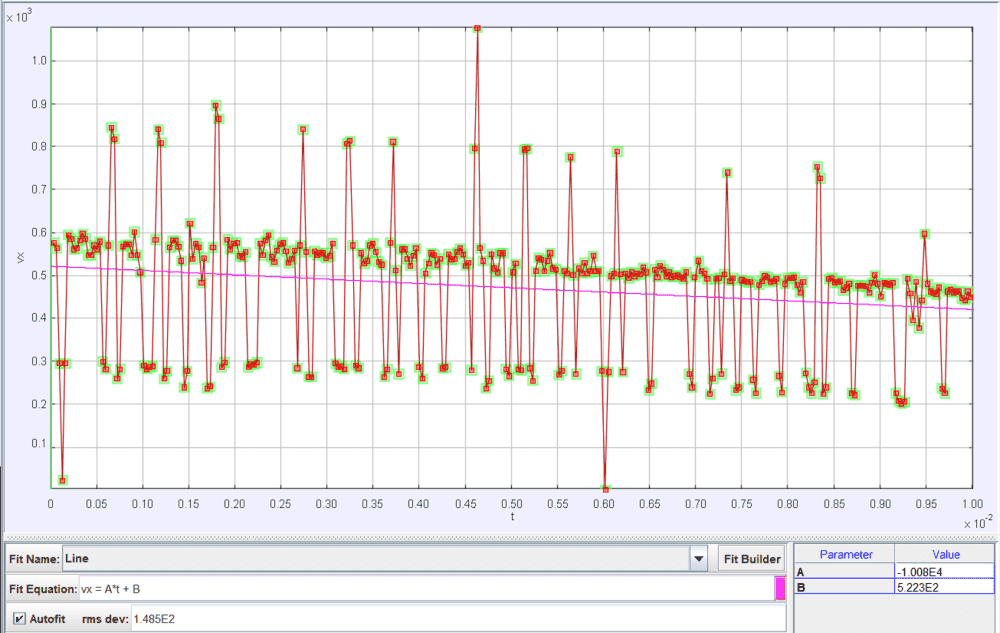
Our measurements of the speed of the ball are consistent with what Destin mentions in the video, and with the angle of the Mach cone, so I'm pretty sure we got the scale and frame rate set up correctly. From the velocity graph below you can see there are some issues with the video quality, probably caused by capturing it from YouTube, then Screencastify, but they seem to average out if we choose a suitable graph.

If anyone here can help with an explanation, I'm very interested.

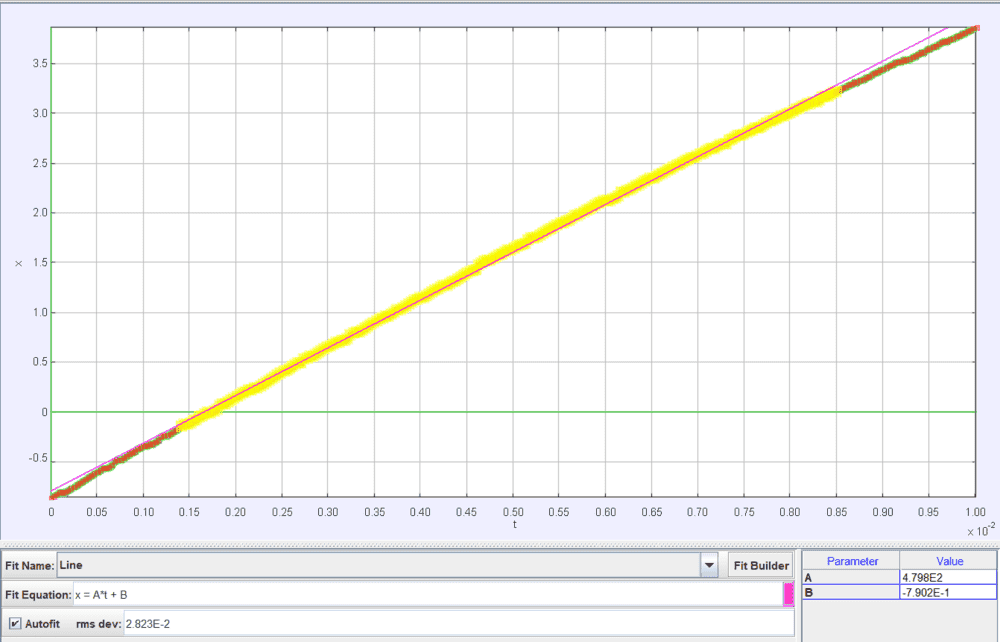
Below is the position graph. The average speed is around 480 m/s, in the same ballpark as the Mach 1.3 Destin states in the video.

The velocity graph below shows the average velocity dropping from just over 500 m/s to just over 400 m/s in around 10 ms, a bigger drop than we were expecting.

 

[.Scott]

Was the video shot with a flat field lens?
If not, there may be slight optical distortion.

 

[.Scott]

I believe you are using the video that starts at 18:00.
For the measurements you are making, it would be critical for the sensor plane of the camera to be precisely parallel to the line of flight of the ball. They don't seem to have set it up that way.

 

[mabraden]

Judging from the lack of distortion in the corners of the slow motion video, I don't think the lens would cause too much trouble.

As for the position and orientation of the camera, the camera seems to point straight at us while the stakes are lined up across, almost lining up with the plane of the image. The barrel of the gun, on the other hand does look odd pointing out of the screen. But if this is how things were actually arranged for the moving ball, we would see the ball shrinking as it recedes from the camera, which if it happens isn't too significant. Looking at the video a few seconds later, the barrel doesn't look misaligned, so I'm guessing his mobile camera has more significant distortion at the edges.

Also, consider that I'm looking for an explanation for the acceleration being higher than expected, by 3 times. Misalignment of the camera axis from the path of the ball will cause measured velocities to be lower by the cosine of the angle, and can't make them higher. The acceleration will be similarly reduced.

Thanks for making me think.

 

[.Scott]

If the camera plane is tilted away from the gun, the ball will appear to slow as it moves across the screen. If it is tilted towards the gun, it will appear to accelerate.

Ideally, a vertical aerial view would show us the layout very clearly. Lacking that, the best layout view is at 17:51 where it shows the camera looking straight across at the first stake. So if that first stake was in the center of the photo, it would indicate that the camera plane was parallel to the ball's trajectory. But it is not, it is well to the left of the center of the frame. So the camera is yawed to the right, away from the gun.

Just from looking at the 17:51 and 18:02, I would say that the camera is about 28 feet from the stakes and he's using a 50mm lens. So here is my best estimate of the setup:

In this diagram, I have the camera tilted 8.5 degrees. The dashed lines show the camera focal plane as it crosses through each stake. The second stake is deeper into the camera field - and will therefore appear proportionately smaller and slower.

More precisely, in my scenario stake 1 is 27.69 feet into the field and stake 2 is 29.47 feet into the field. So the ball would track across the screen 6.4% slower at stake 2 even if it had not decelerate at all.

 

[boneh3ad]

This is an awful lot of hand-wringing over a 6% error considering @mabraden said his $C_D$ is a factor of 3 larger than he/she expected.

Ultimately, the drag is high due to wave drag from the shock wave. You suggest you expected $C_D$ to be about 1/3 of what you have calculated. What is your source on that?

 

[.Scott]

This is an awful lot of hand-wringing over a 6% error considering @mabraden said his $C_D$ is a factor of 3 larger than he/she expected.

His chart shows a drop in velocity from 520 to 420. From my rough estimate, it would actually be a drop from 520 to 447. I am not attempting to convert that to a $C_D$, but I'm sure it takes a chunk out of his 3.0.

Also, 28 feet is likely a significant overestimate of the camera distance. A more accurate way of determining the camera distance would have been to presume a 50mm lens and backout the distance based on how far apart the stakes appear from each other in the frame.

Ultimately, the drag is high due to wave drag from the shock wave. You suggest you expected $C_D$ to be about 1/3 of what you have calculated. What is your source on that?

I don't understand the "1/3 of what have calculated".
My thesis is only that $C_D = 3$ is likely inaccurate. Not that it is supposed to be 1.
I am trying to be responsive to the OP.

 

[boneh3ad]

I was asking @mabraden for his source.

 

[mabraden]

It was hard to find sources of information on drag coefficients for this situation. Most of what I found was for low Reynolds numbers. I calculated a Reynolds number of around 2e6 (based on an average speed of 480 m/s, size of 0.076 m, and air dynamic viscosity of 15.52e-6 m^2/s) which I can now call high after seeing the research available.

Here's a giant study (Free-Flight Measurements of Sphere Drag at Subsonic, Transonic, Supersonic, Hypersonic Speeds, ...,Bailey and Hiatt, 1979), the only appropriate one I found, that includes supersonic motion at high Reynolds numbers. Page 56 is where you'll see that an object with a Reynolds number of 2e6 has a coefficient of around 1 or less, as shown.

Here's my calculation of the coefficient from the baseball data.
C_d = \frac{2ma}{\rho v^2 A} = \frac{2(0.145 kg)(10 000 m/s^2)}{(1.27 kg/m^3)(480 m/s)(\pi(0.037 m)^2)} = 2.3
This coefficient is more than double (sorry, not triple!) the expected value.

Here's why I stated that the value should be around 3, when here I'm saying 2.3, in case you care. I had forgotten that we had played around with the idea of using data only along the central trend on the velocity graph versus all of it. The regression shown in the first post uses all of it, which has a slightly less extreme slope than the central trend, so we get a lower acceleration of 10 000 m/s^2, and a smaller coefficient.

I've come across the term "wave drag" a couple of times in my searches so I'll have to do some more digging. I suppose that wave drag would have to be independent of the drag coefficient, as in another force term to deal with? Could it also depend on how the object is changing speed and interacting with a shock wave? We'll see! The Schlieren image from SmarterEveryDay looks complicated with waves all over the place.

 

[boneh3ad]

So here is the thing: I agree with you that $C_D=3$ or even $C_D = 2.3$ seems high to me. If you use the numbers that @.Scott suggested (which I still think were determined using a lot of conjecture about the alignment that cannot be confirmed), you'd still have $C_D=1.6$, which is higher than I would expect based on the available literature (and the paper you cited is the one I know of with data in this general range of parameters). It's possible there was more misalignment than he estimated or that there is another source of error here.

I don't know anything about the software you are using, but make sure you are familiar with how it works. I'd also point out that the AEDC study used what were essentially ball bearings, i.e. they had smooth, precision-ground surfaces, whereas a baseball has seams that stick up and introduce drag (and likely more wave drag). It's very possible that this combined with the possibility of misalignment of the camera could affect your answer compared with the study you cite (measured $C_D$ too high due to measurement error, actual $C_D$ higher than the AEDC study due to additional sources of drag).

Wave drag is simply a "new" component of drag (relative to subsonic flows) due to the formation of shock waves. It can still be baked into a drag coefficient.

 

[mabraden]

Thanks. I agree that at this point I'd have to evaluate the uncertainty more to see if there's really that much of a disagreement between the calculated coefficient and reasonable values, and I appreciate the suggestions for why it could still be higher than expected (not a smooth sphere, wave drag).

Thanks, everyone, for your input.

 

[boneh3ad]

Thanks. I agree that at this point I'd have to evaluate the uncertainty more to see if there's really that much of a disagreement between the calculated coefficient and reasonable values, and I appreciate the suggestions for why it could still be higher than expected (not a smooth sphere, wave drag).

Thanks, everyone, for your input.

The paper you cited includes wave drag. I was just concerned you might have been comparing the $C_D$ here to more easily finable subsonic sphere data, which do not experience wave drag.