tmilford
- 3
- 0
Homework Statement
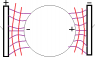
Draw the electric field lines and equipotential lines for the electrode configure. Assume one of the parallel plate is at a positive potential and the other one is grounded.
Homework Equations
The Attempt at a Solution
I know the electric field lines and equipotential lines are perpendicular. I drew the lines but am not 100% sure it's correct. I mainly have problems with the equipotential lines
Here's the original picture
http://i1209.photobucket.com/albums/cc394/alliereid1/original.png
And this is my attempt. The purple lines are the equipotential lines and the left side is positive, and black lines are the electric field lines
http://i1209.photobucket.com/albums/cc394/alliereid1/equipotential.png
It'd be great if someone could look it over to see if I'm on the right track. Thanks!