bonannic
- 3
- 0
Homework Statement
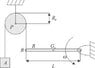
At the instant shown, the rod R is rotating about its centre of rotation with ω=3.8rad/s.
mA=10kg;
The pulley, with mP=8.7kg and RP=0.2m, may be modeled as a uniform disc.
The rod, with mR=4.1kg and L=0.8m, may be modeled as a thin beam rotating about one end.
g=9.8m/s ².
What is the magnitude of the acceleration of point B at this instant?
Homework Equations
ΣF=ma (N2) ΣM=Iα (Eulers equation)
The Attempt at a Solution
IP=(1/2)MR2
IRod at centre of rotation=(1/3)ML2
I defined upwards and anticlockwise to be positive and thus derived the following equations:
ΣFA=TA-mAg=mAaA
ΣMP at centre=RpTA-RpTB=IPαP
ΣMRod at end=-LTB+(1/2)LMRg=IRαR
where TA= Tension force acting between A and pulley and TB=Tension force acting between rod and pulley
I then found these constraints on aB in terms of aA,αP,αR
-aB=aA
5aB=αP
(-5/4)aB=αR
assuming that aB is acting upwards
Then, by subbing aB into the three original equations, I got the following system of equations:
TA+mAaB=mAg
RpTA-RpTB-5IPaB=0
-LTB+(5/4)IRaB=-(1/2)LMRg
However, when I solve this system of linear equations I get the wrong answer. I have a feeling this is because I ignored the angular velocity of the rod but I can't see that would affect the acceleration of B.