stunner5000pt
- 1,443
- 4
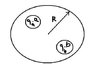
Two spherical cavities of radii a and b are hollowed out from the interior of a neutral conducting sphere of radius R. At the center of each cavity is a point charge place, callthem qa and qb
a) Find teh surface charges sigma a, sigma b, and sigma R.
ok say for qa
\vec{E} = \frac{q_{a}}{4 \pi \epsilon_{0} a^2} \hat{a} = - \vec{\nabla} V \bullet \hat{n}
also \sigma = -\epsilon_{0} \vec{\nabla} V \bullet \hat{n} = \frac{q_{a}}{4 \pi a^2}
but i was told this answer should be negative.. where is my mistake?
a) Find teh surface charges sigma a, sigma b, and sigma R.
ok say for qa
\vec{E} = \frac{q_{a}}{4 \pi \epsilon_{0} a^2} \hat{a} = - \vec{\nabla} V \bullet \hat{n}
also \sigma = -\epsilon_{0} \vec{\nabla} V \bullet \hat{n} = \frac{q_{a}}{4 \pi a^2}
but i was told this answer should be negative.. where is my mistake?