AnonBae
- 8
- 0
Homework Statement
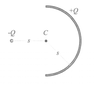
A thin semicircular rod has a total charge +Q uniformly distributed along it. A negative point charge -Q is placed as shown. (Point C is equidistant from -Q and from all points on the rod.)
*Image Attached*
Let Ep and Er represent the electric fields at point C due to the point charge and the rod respectively.
a) Is the magnitude of Ep greater than, less than, or equal to the magnitude of Er? Explain.
b) Is the magnitude of the net electric field at point C greater than, lessthan, or equal to the magnitude of Ep? Explain.
Homework Equations
ΣE = Fe / q
The Attempt at a Solution
a. I am guessing the magnitude of Ep is greater than the magnitude of Er since we can treat a segment charge on the rod as a point charge, and thus the by the equation, the electric field is dependent on the charge. The fractional charge on the rod will produce a greater electrical force than the point charge does.
b. The magnitude of the net electric field is equal to the magnitude at Ep since the point C lies on the electric field line between point C and the fractional charge on the rod.