Electric field at the center of a square homework

[erik-the-red]

Question:

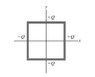
Electric charge is distributed uniformly along each side of a square. Two adjacent sides have positive charge with total charge + Q on each. Each side of the square has length a.

Image at bottom.

Part A:

Suppose the other two sides have negative charge with total charge - Q on each. What is the x-component of the net electric field at the center of the square? Give your answer in terms of Q, a, and epsilon_0.

The electric field at the origin would point away from the positive charge and point towards the negative charge. The x-components would both be in the -x direction and equal in magnitude.

I thought all I had to do was double the equation for an electric field with Q as the charge and (.5a) as the distance.

My answer was - (2)*(Q) / (Pi* a^(2) * (epsilon_0).

Because this is a Mastering Physics question and I was close, my feedback was "Your answer is off by a multiplicative factor."

What did I do wrong?

 

[Saketh]

I thought all I had to do was double the equation for an electric field with Q as the charge and (.5a) as the distance.

You can't just double it. Since each side is a charged rod, you will have to find the electric field a distance .5a away from a charged rod. What you did would work if it were a point charge.

 

[erik-the-red]

I exceeded my attempts (five) on the first part. It was the same as the second part, so I ended up getting 3/4s of the points.

I don't understand why the answer is -\frac{\sqrt{2} \cdot Q}{\pi \cdot a^2 \cdot \epsilon_0}.