Potatochip911
- 317
- 3
Homework Statement
This is problem 4.13 from Griffiths. A long cylinder of radius a carries a uniform polarization P perpendicular to its axis. Find the electric field inside the cylinder.
Homework Equations
##\int \vec{E}\cdot dA = q_{encl}/\varepsilon_0##
The Attempt at a Solution
[/B]
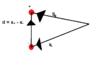
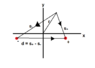
We solve the problem by using a positive and negatively polarized cylinder:
Using Gauss' law we find
$$ \vec{E}(2\pi \vec{s} l) = \frac{\rho \pi \vec{s}^2 l}{\varepsilon_0} \\ \Rightarrow \vec{E} = \frac{\rho}{2\varepsilon_0}\vec{s}$$
then
$$\vec{E_+} = \frac{\rho}{2\varepsilon_0}\vec{s_+} \\ \vec{E_-} = -\frac{\rho}{2\varepsilon_0}\vec{s_-}$$
Summing together gives
$$\vec{E} = \frac{\rho}{2\varepsilon_0}\left(\vec{s_+} - \vec{s_-} \right)$$
and since for dipoles we define the vector ##\vec{d}## going from the negative to the positive charge ##\vec{d} = s_+ - s_-##
$$\vec{E} = \frac{\rho \vec{d}}{2\varepsilon_0} = \frac{\vec{P}}{2\varepsilon_0}$$
However, in the solutions manual they claim ##\vec{d}## is going from the negative to the positive axis and that ##\vec{s_+}-\vec{s_-} = -\vec{d}## which I am having a hard time believing as from a simple diagram this seems incorrect.