Martin V.
- 10
- 0
Homework Statement
Problem statement:
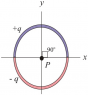
In the attached figure, two curved plastic rods, one of charge q and the other of
charge q, form a circle of radius R 8.50 cm in an xy plane. The x-axis passes
through both of the connecting points, and the charge is distributed uniformly on
both rods. If q 15.0 pC, what are the (a) magnitude and (b) direction (relative to
the positive direction of the x axis) of the electric field produced at P, the center of the circle?
Homework Equations
The Attempt at a Solution
[/B]Read solution on Chegg.com
My question:
Why is it that the electric field only have a component in the x-axis?