haha1234
- 109
- 0
Homework Statement
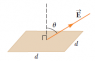
Find the electric flux through the plane surface shown in the figure below if θ = 64.2°, E = 375 N/C, and d = 4.70 cm. The electric field is uniform over the entire area of the surface.
Homework Equations
The Attempt at a Solution
By using the equation:EAcosθ
375x0.0472cos64.2=0.167
I've found that answer is 0.167N.m2/C,but it is not correct.
What is the correct answer?
Attachments
Last edited: