ciso112
- 14
- 2
Homework Statement
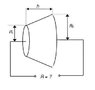
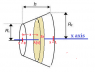
Homogeneous body with the shape of a truncated rotating cone has a base shaped like a
circle. The radius of the lower base is R2 = 8 cm and radius of the upper base is R1 =
4 cm. The height h = 8 cm (see figure). Calculate the total electric
resistance between the base surfaces of the body, when made of a material of
resistivity ρ = 4*10 ^(-2) Ohm*m. Assume that during the transport of electric charge
through the body volume, the current density changes.
Homework Equations
see the picture
The Attempt at a Solution
idea:
triple integration..one through the height...and the remaining ones through the radius and the perimeter...but does this take into account the changing of the radius at different heights?
Attachments
Last edited: