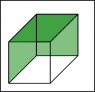
- #1
Rimantas B.
- 3
- 0
Homework Statement
There is a cube with a side length of 0,2m. Its three adjacent walls bear an area charge of -2nC/m2.
Find the strength of the electric field at the center of the cube.
Homework Equations
[tex]E = \frac{\sigma}{2 \varepsilon _{0}} [/tex]
[tex]dE = \frac{\sigma dS}{4 \pi \varepsilon _{0} r^{2}} [/tex]
The Attempt at a Solution
My problem is that I can think of two methods to solve this and get wildly different results.
First attempt:
The first equation is for an infinite plane. However, the walls of the cube are finite. We could say that each of the walls takes 1/6 of the total field of view, so the field strength of each wall would be [tex]E _{1} = \frac{\sigma}{12 \varepsilon _{0}} [/tex].
Then, using vector addition, we can reason that [tex] E _{total} = \sqrt{3} E_1 [/tex] as they are all perpendicular to each other.
This gives a total field strength of about 65 V/m.
Second attempt:
We could use an area integral to obtain [tex] E_{1}[/tex]. Because of the symmetry, the components of the field not perpendicular to the walls cancel each other out, therefore we can only care about the perpendicular ones. That gives us
[tex]dE = \frac{\sigma cos(\alpha) dS}{4 \pi \varepsilon _{0} r^{2}} = \frac{\sigma d dx dy}{4 \pi \varepsilon _{0} r^{3}} [/tex]
herein [tex]d[/tex] is the fixed distance in one axis from the wall to the center - that is, [tex]\frac{a}{2}=0,1m[/tex]
Placing the center of the coordinate system in the center of the wall, we can integrate from x=-0,1 to 0,1 and y=-0,1 to 0,1.
Doing this gives a result more than ten times smaller than the previous method.
Which is correct, if any?