hopkinmn
- 22
- 0
Homework Statement
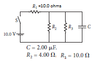
The problem first asks to find potential difference across the capacitor after the switch has been closed a long time. Then it asks to determine the energy stored in a capacitor when the switch has been closed for a long time. I got both these answers right, with Vcapacitor=2.22V and Energy in capacitor=4.9284*10^-6 Joules.
The last part asks to determine how much energy has dissipated through R3 after the switch has been opened.
Homework Equations
The Attempt at a Solution
I know that Power(P)=Current(I)*Voltage(V)=(delta charge)/(delta time)*V and that Power is the derivative of Energy. However, no charge is provided and no time is provided (we just know that it's been a long time), so I'm not sure how to go about solving this problem.
The right answer for the energy dissipated through R3 is 1.41*10^-6 Joules