Frankie
- 2
- 3
- Homework Statement
- I need the demonstration of the simple pendulum "hourly law".
- Relevant Equations
- I've attached images
I've just studied simple pendulum: The simple pendulum (for small oscillations) differential equation is first image.
I've no problem to arrive this result and formula.
My problem is to get to the second formula by passing through another formula (Image 3) that my book mentions. I can't understand the passage.
Image 3 refers to acceleration expressed as a function of the position, is a simple harmonic motion.
In the image 3 last formula refers to centre where x0 = 0 and v0=ωA
My book: "For small oscillations the diffential equation becomes that of image 1 and coincides with that of the simple harmonic motion shown in image 3 set ω2 = g / L.
In conclusion, the motion of the pendulum is harmonic oscillatory when the amplitude of the oscillations is small so that senθ ≅ θ"
And then arrives at image2.
I would need to switch from the first to the second formula.
Thank you in advance.
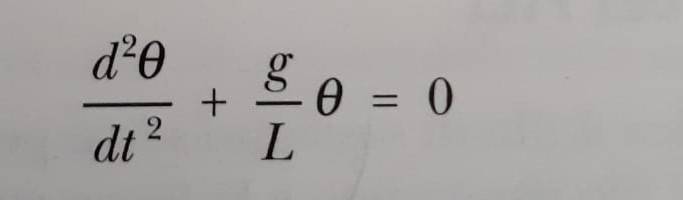 Image 1
Image 1
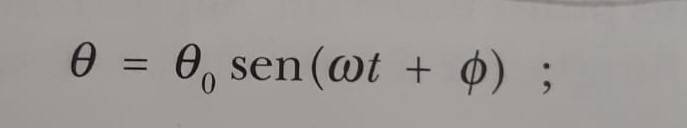 Image 2
Image 2
 Image 3
Image 3
I've no problem to arrive this result and formula.
My problem is to get to the second formula by passing through another formula (Image 3) that my book mentions. I can't understand the passage.
Image 3 refers to acceleration expressed as a function of the position, is a simple harmonic motion.
In the image 3 last formula refers to centre where x0 = 0 and v0=ωA
My book: "For small oscillations the diffential equation becomes that of image 1 and coincides with that of the simple harmonic motion shown in image 3 set ω2 = g / L.
In conclusion, the motion of the pendulum is harmonic oscillatory when the amplitude of the oscillations is small so that senθ ≅ θ"
And then arrives at image2.
I would need to switch from the first to the second formula.
Thank you in advance.