Lord Dark
- 120
- 0
Homework Statement
Hi again ,, My third Question of the day :
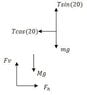
A 250-kg block is supported by a cable attached to a rod of mass 100 kg that can pivot
at the base.
a) Calculate the tension in the tie-rope between the rod and the
wall if it is holding the system in the position shown in Figure.
b) Find the horizontal and vertical forces exerted on the base of
the rod.
Homework Equations
The Attempt at a Solution
in the attachment you'll see the forces I assigned to the system ,, is it right ?? or should I have T2 (above mg) ?? if not I think the question will be too easy:
Fnet(x)=Fh-Tcos(20)
Fnet(y)=Fv+Tsin(20)-mg-Mg (but Tsin(20) = mg) so i can get T and Fv and Fh without even using the Torque ,, so any ideas ??