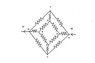
Equivalent resistance across a circuit made of 12 resistors

[opencircuit]

hey can anybody please tell me how to solve this circuit??

I tried this sum out but I can't understand which points are symmetrical and have same potential..or how the current is distributed

 

[Stonebridge]

The symmetry means that potential at C=D=E=F = 0.5 the pd between A and H
This means there is no current through the arms CD and FG. So you can ignore the 2 resistors there.
This allows you to simplify the circuit using series and parallel resistors.

 

[opencircuit]

ok, I solved the combinations and I got 3/4 R.
but what if the circuit is not symmetrical..that is if we have to find the equivalent resistance between A and B?

 

[Stonebridge]

I also get 3/4 R.
If the circuit is not balanced, I can't see much use for it! Usually, these "bridge" type circuits are only useful when balanced. [eg Wheatstone bridge]

To attempt to answer the question, though, one possibility would be to set up a system of Kirchhoff's Law equations for the various closed loops (where ΣIR = 0) as well as the main circuit supplying the pd that provides the main current.
You would get 6 equations with 6 unknowns and a relationship between the main current and the applied pd. This would give the equivalent R.

 

[rwisz]

I would suggest approaching this circuit problem by using the principles of Ohm's Law and Kirchhoff's Laws. These laws state that in a series circuit, the total resistance is equal to the sum of individual resistances, and in a parallel circuit, the total resistance is less than the smallest individual resistance.

To solve this circuit, you can start by identifying which resistors are in series and which are in parallel. In a series circuit, the current remains constant throughout, so the current passing through each resistor will be the same. In a parallel circuit, the current is divided among the branches, so the total current will be equal to the sum of the currents in each branch.

After identifying the series and parallel sections of the circuit, you can use the equations for equivalent resistance in series and parallel to calculate the total resistance of the circuit. Once you have the total resistance, you can then use Ohm's Law (V=IR) to calculate the current passing through each resistor.

As for identifying symmetrical points and potential, this would require a deeper understanding of the circuit and its components. You may need to use Kirchhoff's Laws, which state that the sum of all currents entering a junction is equal to the sum of all currents leaving the junction, and the sum of all potential differences in a closed loop is equal to zero.

In summary, to solve this circuit, you will need to apply the principles of Ohm's Law and Kirchhoff's Laws, as well as identify the series and parallel sections of the circuit. It may also be helpful to draw a schematic diagram to better visualize the circuit and its components.